Анализ задачи
1 Статическая сторона
Уравнения равновесия узла О можно представить в виде
 (1)
(1)
Следовательно, при n=2, если оба стержня не лежат на одной прямой, система геометрически неизменяема и статически определима.
При n >2 система статически неопределима. Степень статической неопределимости S= n-2. В последнем случае для определения усилий в стержнях необходимо учесть их деформативность.
2 Кинематическая сторона задачи
Под действием нагрузки F стержни деформируются и узел О получит перемещение, проекции которого на оси X и Y u и υ соответственно (рис. 2). Откуда абсолютная деформация i-го стержня:
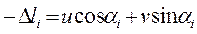 (2)
(2)
3 Физическая сторона задачи
Полагая деформации линейно - упругими, имеем
 где
где 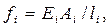 (3)
(3)
Таким образом, для отыскания n неизвестных усилий Ni, n неизвестных деформаций Δli и двух компонент перемещения узла u и υ (всего 2n+2 неизвестных) получено 2 уравнения равновесия (1), n геометрических соотношений (2) и n физических уравнений (3) (всего 2n+2 уравнений). Следовательно, система 2n+2 линейных уравнений относительно 2n+2 неизвестных позволяет однозначно их определить.
4 Синтез полученных зависимостей
а) решение в усилиях
Предварительно преобразуем геометрическое условие (2) включающее и абсолютные деформации стержней и перемещения узла к виду, где перемещения исключены
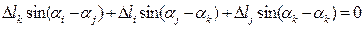 (4)
(4)
являющемуся условием совместности деформаций для каждой тройки k≠i≠j стержней рассматриваемой системы.
Подставляя (3) в (2а) получаем n-2 дополнительные линейные однородные уравнения относительно неизвестных усилий в стержнях
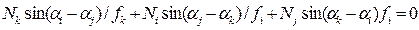 (5)
(5)
Решая совместно линейную систему, состоящую из 2-х уравнений (1) и
n-2 уравнений (5) определяем n неизвестных усилий Ni и по формулам (3) i.
б) решение в перемещениях
В данном случае удобно за основные неизвестные принять перемещения узла О. Для этого необходимо в рассматриваемой системе предварительно исключить неизвестные усилия Ni и деформации Δli.
Подставляя (2) в (3) найдем
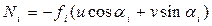 (4)
(4)
подставляя (4) в (1) получим
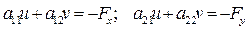 , (5)
, (5)
где
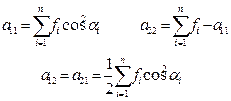 (6)
(6)
Решая (5) находим искомые перемещения u и v, а по формулам (2) и (3) абсолютные деформации i и усилия Ni в стержнях.
Как и в предыдущей задаче, решение в перемещениях предпочтительно при числе стержней n>4.
Контрольные вопросы к лекции 5
1 Как понимать статическую неопределимость задачи сопротивления материалов вообще?
2 Разъясните понятия внутренней и внешней статической неопределимости.
3 Поясните общую схему раскрытия статической неопределимости.
4 Суть и последовательность анализа статической неопределимости задач механики деформируемого тела.
5 Три пути синтеза зависимостей, найденных при анализе.
6 Суть метода сил.
7 Суть метода перемещений.
8 Метод сил и условия совместности деформаций.
9 Метод перемещений и условия равновесия.
10 Поясните метод перемещений на простом примере.
11 Поясните метод сил на простом примере.
12 Поясните метод перемещений на простом примере.
13 Что такое основная система в методе сил и в методе перемещений.
14 Запишите в общем виде канонические уравнения метода перемещений, разъясните физический смысл коэффициентов и свободных членов.
15 Запишите в общем виде канонические уравнения метода сил разъясните физический смысл коэффициентов и свободных членов.
16 Поясните сущность и преимущества использования статически неопределимых основных систем в методе сил.