ГОСУДАРСТВЕННЫЙ ОБРАЗОВАТЕЛЬНЫЙ СТАНДАРТ ПО ДИСЦИПЛИНЕ

МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ И СЕРТИФИКАЦИЯ

ШАХТИНСКИЙ ИНСТИТУТ ЮРГТУ

ЮЖНО-РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

(НОВОЧЕРКАССКИЙ ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ)

(КУРС ЛЕКЦИЙ)

Шахты 2005

УДК 621.01

Составители: Марков В.Ф., Сухарникова В.А., Яцунова Г.К.

Метрология стандартизация и сертификация (курс лекций). / Шахты: Шахт. Инст. Южно-Российского гос. техн. ун-та, 2005.______с.

Рассмотрены общие понятия метрологии и метрологического обеспечения, а также виды и средства измерений. Использованы новые метрологические термины и определения. В сжатом виде освещаются научно-методические и организационные основы Государственной системы стандартизации, правовые и практические вопросы деятельности отечественных и зарубежных организаций по стандартизации, ее принципы и методы, а также стандартизация отклонения геометрических параметров деталей. Излагаются основы сертификации продукции и услуг, технология проведения сертификации и аттестации производства, описываются схемы и системы сертификации.

Разработаны в соответствии с программой дисциплины «Метрология, стандартизация и сертификация» и предназначены для студентов технических специальностей всех форм обучения.

Яцунова Г.К., 2005

«МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ И СЕРТИФИКАЦИЯ»

ОПД.Ф.05

Метрология, стандартизация и сертификация: Теоретические основы метрологии. Основные понятия, связанные с объектами измерения: свойство, величина, количественные и качественные проявления свойств объектов материального мира. Основные понятия, связанные со средствами измерений (СИ). Закономерности формирования результата измерения, понятие погрешности, источники погрешностей. Понятие многократного измерения. Алгоритмы обработки многократных измерений. Понятие метрологического обеспечения. Организационные, научные и методические основы метрологического обеспечения. Правовые основы обеспечения единства измерений. Основные положения РФ об обеспечении единства измерений. Структура и функции метрологической службы предприятия, организации, учреждения, являющихся юридическими лицами. Исторические основы развития стандартизации и сертификации. Сертификация, ее роль в повышении качества продукции и развитие на международном, региональном и национальном уровнях. Правовые основы стандартизации. Международная организация по стандартизации (ИСО). Основные положения государственной системы стандартизации (ГСС). Научная база стандартизации. Определение оптимального уровня унификации и стандартизации. Государственный контроль и надзор за соблюдением требований государственных стандартов. Основные цели и объекты сертификации. Термины и определения в области сертификации. Качество продукции и защита потребителя. Схемы и системы сертификации. Условия осуществления сертификации. Обязательная и добровольная сертификация. Правила и порядок проведения сертификации. Органы по сертификации и испытательные лаборатории. Аккредитация органов по сертификации и испытательных (измерительных) лабораторий. Сертификация услуг. Сертификация систем качества.

часа

1. ОСНОВЫ МЕТРОЛОГИИ

1.1. Понятие метрологии и правовые основы

метрологической деятельности

В процессе познавательной деятельности человека возникает множество задач, для решения которых необходимо располагать количественной информацией о том или ином свойстве объектов. Основным способом получения такой информации являются измерения. Информация о свойствах и качествах объектов, полученная посредством измерений, называется измерительной информацией.

Чтобы успешно справиться с многочисленными и разнообразными проблемами измерений необходимо освоить некоторые общие принципы их решения, нужен единый научный и законодательный фундамент. Таким фундаментом является метрология – наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.

До 1993г. Правовые нормы в области метрологии устанавливались постановлениями Правительства. В 1993г. Принят Закон РФ «Об обеспечении единства измерений».

Цели этого закона заключается в следующем:

- защита прав и законных интересов граждан, экономики РФ от отрицательных последствий недостоверных результатов измерений;

- содействие научно-техническому и экономическому прогрессу на основе применения государственных эталонов единиц величин и использование результатов измерений гарантированной точности, выраженных в допускаемых к применению в стране единицах;

- создание благоприятных условий для развития международных и межфирменных связей;

- регулирование отношений государственных органов управления РФ с юридическими лицами по вопросам изготовления, выпуска, эксплуатации, ремонта, продажи и импорта средств измерений.

Закон устанавливает и закрепляет основные понятия, принимаемые для целей Закона:

- единство измерений – состояние измерений, при котором их результаты выражены в указанных единицах величин и погрешности измерений не выходят за установленные границы с заданной вероятностью;

- поверка средства измерения – совокупность операции, выполняемых органами государственной метрологической службы, с целью определения и подтверждения соответствия средства измерений установленным техническим требованиям;

- калибровка средства измерений – совокупность операции, выполняемых с целью определения и подтверждения действительных значений метрологических характеристик и пригодности к применению средства измерений, не подлежащего государственному метрологическому контролю и надзору;

- сертификат об утверждении типа средств измерений – документ, выдаваемых уполномоченным на то государственным органом, удостоверяющей, что данный тип средств измерений утвержден в порядке, предусмотренном законодательством, и соответствует установленным требованиям;

- аккредитация на право поверки средств измерений – официальное признание уполномоченным на то государственным органом полномочий на выполнение поверочных работ;

- лицензия на изготовления(ремонт, продажу, прокат)средств измерений – документ, удостоверяющий право заниматься указанными видами деятельности, выдаваемый юридическим и физическим лицам органом государственной метрологической службы.

Закон служит базой для создания в России новой системы измерений, которая может взаимодействовать с национальными системами измерений зарубежных стран. Это необходимо для взаимного признания результатов испытаний и сертификации. В сферах, которые не контролируются государственными органами, создается Российская система калибровки, направленная на обеспечения единства измерений. Вводится лицензирование метрологической деятельности, что связано с защитой прав потребителя. Право выдачи лицензии предоставлено исключительно органам Государственной метрологической службы. Закон вводит определенную систему сертификации средств измерений на соответствие метрологическим нормам правилам, а также требования Российской системы калибровки средств измерений.

Во исполнение принятого Закона Правительство РФ в 1994г. утвердило ряд документов: «Положение о государственных научно-метрологических центрах», «Порядок утверждений о метрологических службах федеральных органов исполнительной власти и юридических лиц», «Порядок аккредитации метрологических служб юридических лиц на право поверки средств в изменении» и др.

Закон РФ «Об обеспечении единства измерений» предусматривает юридическую ответственность нарушителей метрологических правил и норм. Закон устанавливает различные меры пресечения или предупреждения нарушений (запреты, обязательные предписания и др.). Предусматривается также административная, гражданско-правовая или уголовная ответственность. Меры пресечения или предупреждения применяются государственными инспекторами Госстандарта.

Нарушителями могут выступать должностные лица или граждане, зарегистрированные в качестве предпринимателей. При нарушении ими правил поверки измерений, требований к состоянию эталонов, установленных единиц, величин или метрологических правил и норм в торговле, а равно выпуск, продажа, прокат и применение средств измерений, типы которых не утверждены, либо применение не поверенных средств измерений влекут штрафные санкции в размере от пяти до ста минимальных размеров оплаты труда.

1.2. Физическая величина

Целью измерения и его конечным результатом является нахождение значения физической величины. Значение физической величины – оценка физической величины в принятых для измерения данной величины единицах.

В теории измерений вводится понятия истинного измеряемого и действительного значения физической величины существует, однако определить его путем измерений невозможно. Поэтому в практике измерений оперируют понятием действительного значения.

Действительное значение – значение физической величины, найденное экспериментальным путем и настолько приближающееся к истинному, что для данной цели может быть использовано вместо него.

Измеряемая физическая величина – физическая величина, подлежащая измерению в соответствии с поставленной измерительной задачей.

Влияющая физическая величина – физическая величина непосредственно не измеряемая средством измерения, но оказывающая влияние на него или на объект измерения таким образом, что это приводит к искажению результата измерения.

Постоянная величина – физическая величина, размер которой по условиям измерительной задачи можно считать не изменяющимся за время, превышающее длительность измерения.

Переменная величина – физическая величина, изменяющаяся по размеру в процессе измерения.

Погрешность измерения есть отклонение результата измерений от истинного значения измеряемой величины. Абсолютной погрешностью называют погрешность измерения, выраженную в единицах измеряемой величины: , где х – истинное значение измеряемой величины. Относительная погрешность – отношение абсолютной погрешности измерения к истинному значению физической величины:.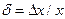

Так как истинное значение измерения остается неизменным, на практике можно найти лишь приближенную оценку погрешности измерения. При этом вместо истинного значения принимают действительное значение физической величины, полученное при измерениях той же величины с более высокой точностью. Точность измерений может быть выражена количественно как обратная величина модуля относительной погрешности. Например, если погрешность измерения , то точность измерения равна 100.

1.3. Виды измерений

Измерение – нахождение значения физической величины опытным путем с помощью специальных технических средств.

Измерения, как экспериментальные процедуры весьма разнообразны и классифицируются по разным признакам.

По способу нахождения искомого значения измеряемой величины различают прямые, косвенные, совместные и совокупные измерения.

Прямое измерение – измерение, при котором искомое значение величины находят непосредственно по показаниям средства измерения.

Косвенное измерение – измерение, при котором искомое значение физической величины рассчитывают по формуле, а значения величины, входящих в формулу, получают измерениями.

Совместные измерения – одновременные измерения двух или нескольких разнородных величин для установления зависимости между ними (ряд одновременных, прямых измерений электрического сопротивления проводника и его температуры для установления зависимости сопротивления от температуры).

Совокупные измерения – производимые одновременно измерения нескольких одноименных величин, при которых искомые значения величин находят решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин (нахождение значений массы отдельных гирь набора по известному значению массы одной из гирь: сравнивая массы различных сочетаний гирь, получают систему уравнений, из решения которых находят массу каждой из гирь, входящих в набор).

По характеру изменения измеряемой величины в процессе измерений бывают статистические, статические и динамические измерения.

Статистические измерения связаны с определением характеристик случайных процессов, звуковых сигналов, уровня шумов и т.д.

Статические измерения имеют место тогда, когда измеряемая величина практически постоянна.

Динамические измерения связан с такими величинами, которые в процессе измерений претерпевают те или иные изменения.

По количеству измерительной информации различают однократные и многократные измерения.

Однократные измерения – это одно измерение одной величины, т.е. число измерений равно числу измеряемых величин. Практическое применение такого вида измерений всегда сопряжено с большими погрешностями, поэтому следует проводить не менее трех измерений и находить конечный результат как среднее арифметическое значение.

Многократные измерения характеризуются превышением числа измерений количества измеряемых величин. Обычно минимальное число измерений в данном случае больше трех. Преимущество многократных измерений – в значительном снижении влияний случайных факторов на погрешность измерения.

По отношению к основным единицам измерения делят на абсолютные и относительные.

Абсолютными измерениями называют такие, при которых используются прямое измерение одной основной величины и физическая константа. Так в формуле масса (m) – основная физическая величина, которая может быть измерена прямым путем (взвешиванием), а скорость света (с) – физическая константа.

Относительные измерения базируются на установлении отношения измеряемой величины к однородной, применяемой в качестве единицы. Естественно, что искомое значение зависит от используемой единицы измерений ().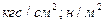

1.4. Методы измерений

Под методом измерений понимают совокупность приемов использования принципов и средств измерений, выбранных для решения конкретной измерительной задачи.

Искомое значение физической величины находится посредством сопоставления ее с мерой, материализующей единицу этой величины. В зависимости от способа применения меры различают методы непосредственной оценки и методы сравнения.

При измерении методом непосредственной оценки искомое значение величины определяют непосредственно по отчетному устройству средства измерения, которое проградуировано в соответствующих единицах.

Метод сравнения с мерой – метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой (Сравнение массы на рычажных весах). Отличительной чертой методов сравнения являются непосредственное участие меры в процедуре измерения, в то время как в методе непосредственной оценки мера в явном виде не присутствует, а ее размеры перенесены на отсчетное устройство (шкалу), при его градуировке.

Метод сравнения с мерой имеет несколько разновидностей: нулевой метод, дифференциальный метод, метод замещения и метод совпадения.

Нулевой метод – метод сравнения с мерой, в котором результирующий эффект воздействия измеряемой величины и встречного воздействия меры на сравнивающее устройство сводят к нулю.

Пример: Измерение массы на равноплечих весах, когда воздействие на весы массы полностью уравновешиваются массой гирь (рис.2.1 а)

При дифференциальном методе полное уравновешивание не производят, а разность между измеряемой величиной и величиной, воспроизводимой мерой, отсчитывается по шкале прибора.

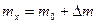Пример: Измерение массы на равноплечих весах, когда воздействие массы на весы частично уравновешивается массой гирь , а разность масс отсчитывается по шкале весов градуированной в единицах массы (рис. 2.1 б). В этом случае значение измеряемой величины , где 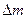- показания весов.

а) б) в)

Рис. 1.1 – Методы сравнения

Метод замещения – метод сравнения с мерой, в котором измеряемую величину замещают известной величиной, воспроизводимой мерой.

Пример: Взвешивание на пружинных весах. Измерение производят в два приема. Вначале на чашу весов помещают взвешиваемую массу и отмечают положение указателя весов; затем массу замещают массой гирь подбирая ее так, чтобы указать весов установился точно в том же положении, что и в первом случае. При этом (рис. 1.1. в).

В методе совпадений разность между измеряемой величиной и величиной воспроизводимой мерой измеряют, используя совпадения отметок шкал.

Пример: Измерение линейных размеров штангенинструментами. При этом используется совпадение основной и отметок шкал.

1.5. Ошибки измерений (Теория ошибок)

Измеряя физическую величину, мы не рассчитываем получить ее истинное значение. Поэтому необходимо указать, насколько полученный результат может быть близким к истинному значению, т.е. указать какова точность измерения:

, это значит от 255,5 до 256,5 (в пределах),

на самом деле это равенство имеет вероятный характер. Мы не можем с полной уверенностью сказать, что величина лежит в указанных пределах, но имеется некоторая вероятность этого.

Например: 200,025 Ом при значима

200,034 Ом при 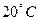ли ошибка

Если ошибка 0,001 Ом, то разница значима.

Если ошибка 0,010 Ом, то разница незначима.

Грубые – это ошибки, выходящие за пределы точности, присущей данным условиям измерений, это просчеты исполнителя, или резкие изменения внешних условий. Их исключают!

Рис. 1.2. Классификация ошибок измерений.

Систематические – величина которых одинакова во всех измерениях, проводящихся одним и тем же методом с помощью одних и тех же измерительных приборов.

Причины: погрешности приборов, изменение температуры (среды). Повторные измерения не позволяют ни обнаружить, ни устранить систематические ошибки (при одних и тех же условиях), поэтому систематические ошибки опаснее случайных. Систематические ошибки можно разделить на 4 группы:

– ошибки, природа которых нам известна и величина может быть достаточно точно определена, их устраняют поправками (нагревание линейки).

– ошибки известного происхождения, но неизвестной величины (учет цены деления шкалы): I = (65,3 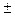0,75) Ма.

– ошибки, о существовании которых мы не подозреваем. Проявляются при сложных измерениях. Измерение плотности металла (образец содержал пустоту). Борьба – необходимо тщательно продумывать методику измерения.

– ошибки, обусловленные свойствами измеряемого объекта. Овальность цилиндра (диаметр), неоднородность материала (электропроводимость) и т.п.

Случайные – величина которых неодинакова в измерениях, проводящихся даже одним и тем же методом.

При отсутствии систематических ошибок они служат причиной разброса повторных измерений относительно истинного значения:

а) Истинное значение

При отсутствии систематически ошибок

б) истинное значение

При наличии систематических ошибок

Рис. 1.3. Графическое изображение систематической ошибки.

Случайные ошибки можно обнаружить путем повторных измерений, их можно вычислить методами математической статистики.

Систематические ошибки не поддаются математическому анализу, их необходимо выявлять и устранять, общих рецептов на этот счет не существует. Если случайная ошибка окажется меньше систематической, то очевидно, что нет смысла пытаться еще уменьшить величину случайной ошибки – все равно результаты измерений не станут от этого заметно точнее, нужно искать пути к уменьшению систематической ошибки.

Правила:

1. Если систематическая ошибка является определяющей, т.е. ее величина существенно больше величины случайной ошибки, присущей данному методу, то достаточно выполнять измерение один раз.

2. если случайная ошибка является определенной, то измерение следует производить несколько раз. Число измерений целесообразно выбирать таким, чтобы случайная ошибка среднего арифметического была меньше систематической ошибки, с тем чтобы последняя опять определена окончательную ошибку результата.

Количественное уточнение дает теория вероятностей, значение которой нужно для оценки величин случайных ошибок.

1.6. Основные понятия теории вероятности

Случайными называются такие события, о появлении которых не может быть сделано точного предсказания.

Вероятность благоприятного события (n)

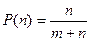
Вероятность неблагоприятного события (m)

Основной закон теории вероятности (закон больших чисел) утверждает, что при достаточно большом числе наблюдений N с вероятностью, близко к достоверности, частота появления события как угодно мало отличается от вероятности этого события, иначе говоря: если , то всегда можно выбрать достаточно большое N, чтобы выполнялось соотношение ,

где - частота появления (n), причем m и n нам неизвестны (К - число белых шаров);

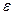- как угодно малое положительное число, отличное от нуля.

Это соотношение дает возможность устанавливать опытным путем с достаточно хорошим приближением, вероятность неизвестного нам случайного события.

При измерениях физических величин в тех случаях, когда основную роль играют случайные ошибки, все оценки точности измерения можно сделать только с некоторой вероятностью.

Допустим, что мы проводим серию измерений одной и той же величины: и т.д. неодинаковы.

Истинное значение обозначим Х.

В качестве наилучшего значения искомой величины выбирается среднее арифметическое

Насколько величина близка к Х? Имеется какая-то вероятность того, что Х лежит в каких-то пределах вблизи .

Рис. 1.4 Разброс результатов измерений.

Чем больше разброс результатов, тем больше должна быть ошибка в величине .

Результаты серии измерений одной величины можно наглядно представить, построив диаграмму, которая показывала бы, как часто получались те или иные значения.

Гистограмма

Интервал, мм	частость
9,9-10,1 10,1-10,3 10,3-10,5 10,5-10,7 10,7-10,9 10,9-11,1 11,1-11,3

Рис. 1.5. Гистограмма результатов измерений.

Допустим, что сделано N равноточных измерений, то можно получить кривую распределения.

Нормальный закон распределения может быть выведен из следующих предложений:

Y– плотность распределения

1 Аксиома случайности. При большом числе измерений ошибки одинаковой величины, но разного знака встречаются одинаково часто.

2 Аксиома распределения. Часто ошибок уменьшается с увеличением величины ошибки.

Для оценки величины случайной ошибки измерения, чаще всего применяется средняя квадратичная ошибка (стандарт), легче определить доверительные вероятности (по таблицам).

(Истинное значение) (n > 30)

Относительная величина средней квадратичной ошибки W, в %, носит название коэффициент вариации:

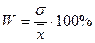
Можно применять и среднюю арифметическую ошибку:

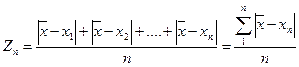
(Истинное значение) для n>30

или

Доверительная вероятность (коэффициент надежности)

Запишем

это означает, вероятность того, это результат измерений отличается от истинного значения Х на величину, не большую, чем .

Интервал значений от до называется доверительным интервалом.

Для характеристики величины случайной ошибки необходимо задать два числа, а именно:

1) величина самой ошибки (или доверительного интервала);

2) Величину доверительной вероятности, знание доверительной вероятности позволяет оценить степень надежности полученного результата.

Пример: Пусть для некоторого ряда измерений мы получим

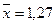Доверительные границы

1.6. Средства измерений

Средства измерений – это технические средства, используемые при измерениях и имеющие нормированные метрологические характеристики, влияющие на результаты и на точность измерений. Средства измерений подразделяются на: меры, измерительные системы, измерительные преобразователи.

Мера – средство измерений, предназначенное для воспроизведения одного или нескольких фиксированных значений физической величины (мера массы – гиря, мера длины – концевая мера).

Однозначная мера воспроизводит физическую величину одного размера, например концевая мера длины и мера массы (гиря). Многозначная мера воспроизводит ряд одноименных величин различного размера, например, штриховая мера длины и угловая мера (многогранная призма). Специально подобранный комплект мер, применяемых не только самостоятельно, но и в различных сочетаниях в целях воспроизведения ряда одноименных величин различного размера, называется набором мер, например наборы плоскопараллельных концевых мер длины и набора угловых мер.

Магазин мер – сочетание мер, объединенных конструктивно в одно механическое целое, в котором предусмотрено возможность посредством ручных или автоматизированных переключателей, связанных с отсчетным устройством, соединять составляющий магазин меры в нужном сочетании. По такому принципу устроены магазины электрических сопротивлений.

К однозначным мерам относят стандартные образцы и стандартные вещества. Стандартный образец - это должным образом оформленная проба вещества, которая подвергается метрологической аттестации с целью установления количественного значения определенной характеристики. Стандартным образом является образец чистого цинка, который служит для воспроизведения температуры по международной температурной шкале МТШ-90.

При пользовании мерами следует учитывать номинальное и действительное значения мер, а также погрешность меры и ее разряд. Номинальным называют значение меры, указанное на ней. Действительное значение меры должно быть указано в специальном свидетельстве как результат высокоточного измерения с использованием официального эталона.

Разность между номинальным и действительным значениями называются погрешностью меры. Величина, противоположная по знаку погрешности, представляет собой поправку к указанному на мере номинальному значению. Поскольку при проверке также могут быть погрешности, меры подразделяют на разряды (1-го, 2-го и т.д.) и называют разрядными эталонами (образцовые измерительные средства), которые используются для проверки измерительных средств.

Измерительный преобразователь – это средство измерений, которое служит для преобразования сигнала измерительной информации в форму, удобную для обработки или хранения, а также передачи в показывающее устройство. Измерительные преобразователи либо входят в конструктивную схему измерительного прибора, либо применяются совместно с ним, но сигнал преобразователя не поддается непосредственному восприятию наблюдателем. Например, преобразователь может быть необходим для передачи информации в память компьютера, для усиления напряжения и т.д. Преобразуемую величину называют входной, а результат преобразования – выходной величиной. Основной метрологической характеристикой измерительного преобразователя считается соотношение между входной и выходной величинами, называемое функцией преобразования.

Измерительный прибор – средство измерения, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем (вольтметр, амперметр). По назначению приборы делят на универсальные, предназначенные для измерения одинаковых физических величин различных объектов, и специализированные, используемые для измерения параметров однотипных изделий (размеры резьбы, зубчатых колес) или одного параметра различных изделий (шероховатость, твердость). По принципу действия, который положен в основу измерительной системы, приборы подразделяют на механические, оптические, оптико-механические, пневматические, электрические, лазерные и др.

Во многих случаях название прибора определяется конструкцией измерительного механизма. Универсальные приборы для линейных измерений с механической измерительной системой делят на: штангенприборы с прерогатива; микрометрические приборы с микрометрическим винтом; рычажно-механические приборы с зубчатыми и пружинными механизмами.

Измерительные системы и установки – это совокупность средств измерений, объединенных по функциональному признаку со вспомогательными устройствами, для измерения одной или нескольких физических величин объекта измерений. Обычно такие системы автоматизированы и обеспечивают ввод информации в систему, автоматизацию самого процесса измерения, обработку и отображение результатов измерений для восприятия их пользователем. Такие установки используют также для контроля производственных процессов.

Измерительные принадлежности – это вспомогательные средства измерений величин. Они необходимы для вычисления поправок к результатам измерений, если требуется высокая степень точности. Например, термометр может быть вспомогательным средством, если показания прибора достоверны при строго регламентированной температуре.

1.7. Погрешности средств измерений

Успех измерений зависит от грамотного использования средств измерений, от знания их свойств. Уже по обозначениям на шкале прибора можно определить с какой погрешностью мы будем измерять, но для этого надо знать формы представления метрологических характеристик.

Совершенные приборы не должны вносить искажения в значения измеряемых ими величин, а если этого нельзя избежать, то они должны допускать возможность учета исключения этих искажений каким либо приемом.

Погрешности средств измерений возникают в результате воздействия большого числа факторов, обусловленных их изготовлением, хранением, эксплуатацией, условиями проведения измерений. Абсолютная погрешность прибора – разность между показаниями прибора и истинным значением измеряемой величины. Однако в связи с тем, что истинное значение величины неизвестно, на практике вместо него используют действительное значение величины.

Приведенной погрешностью прибора является отношение абсолютной погрешности к нормируемому значению, за которое принимают значение, равное верхнему пределу измерений, или диапазону измерений, или длине шкалы, и т.п. Так, для вольтметра с верхним пределом измерений 150 в и абсолютной погрешностью =0,6 в приведенная погрешность, которую обычно выражают в процентах, будет (0,6/150)*100 = 0,4%.

На погрешность средств измерений большое влияние оказывает условия его применения. Условия применения средств измерения, при которых влияющие величины имеют нормальное значение или находятся в пределах нормальной области значений, называют нормальными условиями. Нормальные условия для линейных и угловых измерений - температура , давление 760мм рт. ст., влажность 58%.

Основной погрешностью являются погрешность средства измерений, используемого при нормальных условиях дополнительной погрешностью-изменение действительного значения меры или показания прибора при отклонении одной из влияющих величин за пределы, установленные для нормальной области ее значений. Наибольшая погрешность средства измерений, при которой оно может быть признано годным, называется пределом допускаемой погрешности.

Класс точности средства измерений – это обобщенная характеристика средства измерений, определяемая пределами допускаемых и дополнительных погрешностей, а также другими свойствами средств измерений, влияющими на их точность.