Построение доверительного интервала
Примером интервальной оценки является доверительный интервал. Доверительный интервал - это отрезок, центром которого является точечная оценка числовой характеристики, включающий истинное значение данной числовой характеристики с заданной вероятностью. Эта вероятность называется доверительной вероятностью. Таким образом, доверительный интервал является мерой точности оценки, а доверительная вероятность характеризует ее достоверность. Размер доверительного интервала зависит от того, каким значением доверительной вероятности задается экспериментатор. Чем больше доверительная вероятность, тем шире должен быть интервал, чтобы с заданной вероятностью включать в себя истинное значение числовой характеристики. Часто выбирают значение доверительной вероятности Рд = 0,95, полагая таким образом, что это значение достаточно велико, чтобы считать, что доверительный интервал “практически всегда” накрывает истинное значение. Только иногда, в случае ответственных и очень ответственных исследований полагают Рд = 0,99 и 0,999 соответственно.
Процедура построения доверительного интервала включает в себя два этапа:
- запись вероятностного утверждения относительно некоторой случайной функции, включающей в себя разность или отношение оценки и числовой характеристики. Такая функция несет информацию о степени близости упомянутых величин. Необходимо, чтобы закон распределения функции был известен;
- вероятностное утверждение преобразуется к виду, при котором границы доверительного интервала числовой характеристики представлены в явном виде.
Примерами функций с известным распределением, которые удовлетворяют необходимым требованиям, являются следующие:
1) 
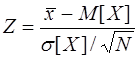, (3.24)
имеющая нормальное распределение, если величина X распределена нормально, а значение s[X] известно;
2) 
(3.25)
имеющая распределение Стьюдента c m = N-1, если величина X распределена нормально, а значение s[X] заранее неизвестно, но его оценка 
может быть получена из опытных данных при помощи формулы (3.23);
3) 
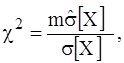(3.26)
имеющая распределение Пирсона с m = N-1, если величина Х распределена нормально.
Напомним, что параметры распределений m являются числами степеней свободы. Кроме того здесь использованы обозначения: 
- cреднее арифметическое значение,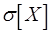 
- среднее квадратическое значение, равное корню квадратному из дисперсии, 
[X] - оценка среднего кадратического значения, определяемая как корень квадратный из несмещенной оценки дисперсии, N - объем выборки.
Функции Z и t могут быть использованы при построении доверительного интервала для математического ожидания, тогда как при помощи функции c2 строится доверительный интервал для дисперсии.
Построим доверительный интервал для математического ожидания при условии, что в нашем распоряжении имеются результаты N наблюдений нормально распределенной величины Х, а среднее квадратическое значение 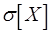заранее известно из независимых наблюдений. Поскольку функция Z распределена нормально, можно использовать соответствующую таблицу для определения значения za, такого, что за пределами - za и + za остается часть площади под кривой распределения в сумме равная a, тогда как в пределах [- za,+ za] заключена часть площади, равная 1 - a . Только что сказанное соответствует следующему вероятностному утверждению:
Р{- za£
£+za }= 1-a. (3.27)
(Вероятность выполнения неравенства, заключенного в фигурных скобках, равна 1-a.). Преобразуем выражение в скобках:
Р{- za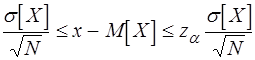
}= 1 - a
или
Р{
(3.28)
Назовем величину 1-a = Рд доверительной вероятностью Рд. Согласно (3.28) при этой доверительной вероятности доверительный интервал для М[X] задается пределами:
. (3.29)
Замечание: К сожалению таблицы нормального распределения в разных книгах строятся неодинаково. Иногда приводится интеграл вероятности
Ф(z) = 
а иногда нормированная функция Лапласа Ф0(z), которая связана с интегралом вероятности соотношением Ф0(z) = Ф(z)/2. Таблицы можно использовать для наших целей, если положить в первом случае a = 1 - Ф(z) , а во втором - a = 1 - 2Ф(z). В обоих случаях za = z . Чтобы избежать неудобств, связанных с промежуточными расчетами, приведем краткую таблицу, которой можно пользоваться непосредственно: