Равномерная функция распределения

Важнейшие функции распределения

Генеральная совокупность и ее характеристики

Случайные погрешности и их оценка

Адекватным математическим аппаратом описания случайных погрешностей является теория вероятностей и математическая статистика. Поэтому уместно здесь напомнить основные понятия этих дисциплин.

Основным объектом теории вероятностей является случайная величина - величина, которая в результате экспериментов принимает различные заранее не известные значения из некоторой совокупности возможных. Случайная величина может быть дискретной и непрерывной. В первом случае она задается набором отдельных значений и соответствующих им вероятностей. Во втором - возможные значения и вероятности задаются непрерывными функциями. Случайная величина в целом задается генеральной совокупностью.

Генеральная совокупность - это полный набор всех возможных значений, которые может принимать случайная величина в ходе эксперимента. Генеральная совокупность может быть конечной и реально существующей (например, рост всех студентов МИРЭА в некоторый момент времени) или бесконечной, гипотетической (например, совокупность всех возможных исходов бросаний игральной кости при бесконечном числе бросаний).

Постулируется, что генеральная совокупность обладает некоторыми неслучайными свойствами, которые надо выявить в результате эксперимента. Исчерпывающей характеристикой случайной величины Х (а следовательно, и генеральной совокупности) является ее функция распределения F(x), равная вероятности того, что в результате эксперимента эта случайная величина примет значение меньшее, чем х. Таким образом:

F(x) = P(X< x). (3.2)

Если функция распределения имеет производную, то функция

f(x) = F¢(x) (3.3)

называется плотностью вероятности.

Как функция распределения F(x), так и плотность распределения f(x) характеризуют всю генеральную совокупность и являются детерминированными, неслучайными функциями, имеющими вполне конкретный аналитический (или графический) вид.

В теории вероятностей и математической статистике важную роль играют следующие функции распределения:

(3.4)

 

Рис.3.2. График функции равномерного распределения

 

Ей соответствует плотность функции распределения:

(3.5)

Рис.3.3. График функции плотности равномерного распределения

2) нормальная функция распределения с параметрами m и s:

, (3.6)

Рис.3.4. График функции нормального распределения

 

которой соответствует плотность распределения:

(3.7)

Рис.3.5. График функции плотности нормального распределения

 

Удобно ввести безразмерную случайную величину:

z = ,

для которой формула (3.7) предстает ее в виде

(3.8)

График функции f(z) представлен на рис. 3.5 зеленым цветом

Произведенное преобразование сохраняет закон распределения, но приводит его к частному виду, соответствующему случаю m = 0 и s = 1.

Говорят, что плотность нормального распределения f(z) является нормированной (площадь под кривой f(z) равна единице), центрированной (максимум находится при z = 0 ), стандартизованной (параметр s = 1);

 

3) функция распределения Стьюдента с параметром m , называемым числом степеней свободы, которая задается плотностью распределения:

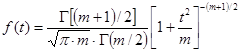, (3.9)

где здесь и ниже Г(*) – гамма функция.

 

f(x)

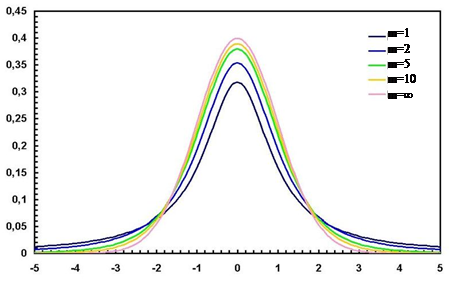t

 

Распределение Стьюдента называют также t - распределением. При достаточно больших значениях m (m>30) оно близко к нормальному распределению f(z). Здесь слово “близко” употреблено в том смысле, что при обычных инженерных экспериментах распределение Стьюдента с m>30 можно заменить нормальным распределением. Вместе с тем при малых m оно значительно отличается от нормального;

 

4) функция распределения Пирсона c² с m cтепенями свободы. Ее плотность вероятности дается формулой:

 

f(c²) = [2^m/2Г(m/2)]^-1(c²)^((m/2)-1)exp(-c²/2), при c²³0 (3.10)

 

f(x)

c²

Рис.3.7. График функции плотности распределения Пирсона ( c² )

 

В отличие от двух предыдущих распределений f(c²) не симметрична и определена только для положительных значений c². При увеличении числа степеней свободы m максимум функции f(c²) сдвигается вправо. Вблизи максимума при больших m функция f(c²) по форме близка к нормальной. Распределение Пирсона со степенями свободы m имеет случайная величина c, представляющая собой сумму квадратов m независимых случайных величин, каждая из которых нормально распределена с m = 0 и s = 1:

c= 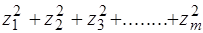. (3.11)

С этим фактом и связано название функции распределения Пирсона как c² - распределения;

 

5) функция распределения Фишера или F- распределение с m₁ и m₂ степенями свободы. Плотность вероятности этой функции равна

f (F) = при F³0. (3.12)

Распределение Фишера имеет случайная величина

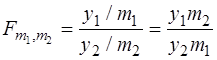(3.13)

где y₁ и y₂ - независимые случайные величины, имеющие c² - распределение с m₁ и m₂ степенями свободы соответственно.

 

Таблицы рассмотренных в этом разделе распределений можно найти в справочниках, посвященных математической статистике.