Характеристики измерений
Классификация измерений
Роль и место измерений в метрологии
Основы метрологии
Измерение является одним из основных понятий метрологии, поэтому классификации и характеристикам измерений уделяется большое внимание. Измерения классифицируют по целому ряду признаков.
По характеристике точности:
Равноточные измерения – ряд измерений какой-либо величины, выполненных одинаковыми по точности средствами измерений в одних и тех же условиях.
Неравноточные измерения – ряд измерений какой-либо величины, выполненных различными по точности средствами измерений и (или) в разных условиях.
По числу измерений, выполняемых в серии:
Однократное измерение – измерение, выполненное один раз. Основным условием, при котором такое измерение в принципе возможно, является наличие априорной информации о точности полученного отсчета.
Многократное измерение – измерение, результат которого получают из нескольких следующих друг за другом измерений, иными словами, измерение, состоящее из ряда однократных измерений. Многократные измерения одной и той же величины постоянного размера производятся при повышенных требованиях к точности измерений.
По характеру изменения во времени измеряемой величины:
Статическое измерение – измерение, на протяжении времени которого измеряемая величина принимается неизменной.
Динамическое измерение – измерение, на протяжении времени которого измеряемая величина принимается переменной.
По метрологическому назначению:
Технические измерения – измерения, выполненные при помощи рабочих средств измерений.
Метрологические измерения – измерения, выполненные при помощи эталонов и образцовых средств измерений. Как правило, такие измерения выполняются с целью воспроизведения единиц физических величин или передачи их размера рабочим средствам измерений. Измерения максимально возможной точности, достигаемой при существующем уровне науки и техники, называют также эталонными, а измерения, погрешность которых с определенной вероятностью не превышает заданного значения и выполняемые метрологическими органами, – контрольно-поверочными.
По способу представления результатов измерений:
Абсолютное измерение – измерение, приводящее к значению, основанному на прямых измерениях одной или нескольких основных величин, и (или) использовании значений физических констант. Результат прямых измерений выражается в единицах измеряемой величины, например, определение длины в метрах, силы электрического тока в амперах, ускорения свободного падения в метрах на секунду в квадрате и т.д.
Относительное измерение - измерение отношения измеряемой величины к одноименной величине, играющей роль единицы или измерение величины по отношению к одноименной величине, принимаемой за исходную. Например, при измерении относительной влажности воздуха, ее определяют как отношение количества водяных паров в 1 куб. см воздуха к количеству водяных паров, которое насыщает 1 куб. см воздуха при данной температуре.
По способу получения (обработки) результатов измерений:
Прямое измерение - измерение, при котором искомое значение физической величины получают непосредственно из опытных данных, например, измерение температуры тела термометром, силы тока – амперметром, длительности временного интервала – секундомером.
Косвенное измерение - измерение, при котором искомое значение физической величины определяют на основании известной зависимости между искомой величиной и другими величинами, значения которых получают в результате прямых измерений. Например, сопротивление резистора R находят из уравнения R=U / I, где падение напряжения на резисторе – U и ток через него – I находят в результате прямых измерений.
Совокупные измерения – измерения нескольких однородных величин в различных их сочетаниях, при которых искомую величину определяют решением системы уравнений. Например, измеряя сопротивления 
 ,
, 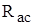 и
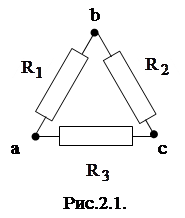
и 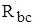 между различными вершинами треугольника, в котором соединены сопротивления
между различными вершинами треугольника, в котором соединены сопротивления 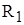 ,
,  и
и 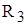 (см.рис.2.1) и, решая систему уравнений (2.1) можно определить искомые значения сопротивлений
(см.рис.2.1) и, решая систему уравнений (2.1) можно определить искомые значения сопротивлений 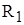 ,
,  и
и 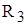 методом совокупных измерений.
методом совокупных измерений.
| 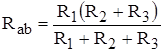
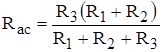 (2.1) (2.1)
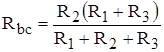 , ,
|
Совместные измерения - одновременные измерения двух или более неоднородных величин для нахождения зависимости между ними. Например, измеряя сопротивление резистора при трех различных температурах, составляют систему из трех уравнений с целью нахождения параметров R0,  и
и  с помощью известной зависимости сопротивления резистора от температуры:
с помощью известной зависимости сопротивления резистора от температуры:
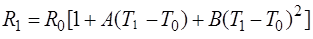
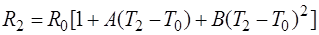
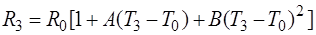
где T0 - температура, при которой определяется значение R0,
A и B - температурные коэффициенты сопротивления,
T1, T2, T3 - текущая температура.
Основными характеристиками измерений являются: принцип измерений, метод измерений, результат, погрешность, точность, сходимость, воспроизводимость, правильность и достоверность.
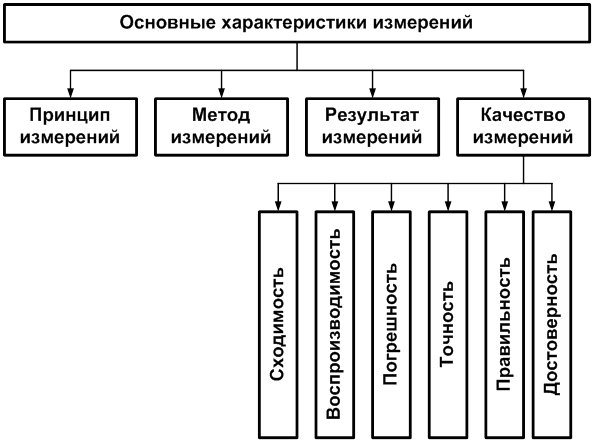
Рис.2.2
Принцип измерений – физическое явление или совокупность физических явлений, положенных в основу измерений.
Метод измерений – совокупность приемов использования принципов и средств измерений. Методы измерений разнообразны.

Основными являются:
Метод непосредственной оценки, при использовании которого искомое значение измеряемой величины получают по показаниям средства измерений, снятых непосредственно с его отсчетного устройства,
Метод сравнения с мерой, при использовании которого искомое значение измеряемой величины получают в результате ее сравнения с величиной, воспроизводимой мерой. Существует целый ряд
Разновидности метода сравнения с мерой:
- метод противопоставления, который характеризуется тем, что измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на устройство сравнения, с помощью которого устанавливается соотношение между этими величинами. Примером реализации этого метода является измерение массы на равноплечих (рычажных) весах с использованием уравновешивающих гирь.
- дифференциальный метод, который характеризуется тем, что на средство измерений воздействует разность между измеряемой величиной и известной величиной, воспроизводимой мерой. Этот метод, при условии высокой точности воспроизведения величины мерой, позволяет получить хорошую точность измерений даже в случае применения относительно неточных средств измерений. Например, необходимо измерить постоянное напряжение, истинное значение которого 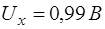 . Возьмем для этого образцовую меру напряжения
. Возьмем для этого образцовую меру напряжения 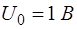 , погрешность которой пренебрежимо мала, и вольтметр с пределом измерения
, погрешность которой пренебрежимо мала, и вольтметр с пределом измерения  и погрешностью, значение которой при измерении величины, равной пределу измерения, составляет
и погрешностью, значение которой при измерении величины, равной пределу измерения, составляет 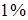 . При использовании дифференциального метода измерений источники измеряемого постоянного напряжения
. При использовании дифференциального метода измерений источники измеряемого постоянного напряжения  и образцового напряжения
и образцового напряжения 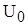 включаются последовательно навстречу друг другу. Разность напряжений
включаются последовательно навстречу друг другу. Разность напряжений 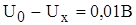 будет измерена с погрешностью
будет измерена с погрешностью 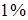 вольтметром с пределом
вольтметром с пределом 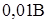 , следовательно, искомое значение напряжения будет определено с относительной погрешностью, равной примерно
, следовательно, искомое значение напряжения будет определено с относительной погрешностью, равной примерно 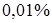 . Эффект повышения точности результатов измерений, достигаемый при использовании дифференциального метода, оказывается тем выше, чем точнее мера воспроизводит значение физической величины.
. Эффект повышения точности результатов измерений, достигаемый при использовании дифференциального метода, оказывается тем выше, чем точнее мера воспроизводит значение физической величины.
- нулевой метод, который характеризуется тем, что измеряемая величина одновременно или периодически сравнивается с мерой, и результирующий эффект воздействия этих величин на устройство сравнения доводится до нуля. Очевидно, что используемая в нулевом методе измерений мера должна быть изменяемой (регулируемой), а точность метода тем выше, чем выше чувствительность устройства сравнения.
- метод замещения, который характеризуется тем, что измеряемую величину замещают известной величиной, воспроизводимой мерой. Например, измерение сопротивления омметром с поочередным подключением к нему измеряемого сопротивления и образцового магазина сопротивлений (регулируемая мера). Сопротивление магазина, при котором показания омметра такие же, как при измерении искомого сопротивления, равно измеряемому значению.
- метод совпадений, который характеризуется тем, что разность значений с размером измеряемой величины и величины, воспроизводимой мерой, определяют, используя совпадение отметок шкал или периодических сигналов. Например, при измерении длины с помощью штангенциркуля с нониусом наблюдают совпадение отметок на шкалах штангенциркуля и нониуса.
Выбор метода измерений зависит от измерительной задачи, наличия необходимых средств измерений, их вида, характеристик, конструктивных особенностей. С целью наилучшей реализации выбранного метода измерений необходимо определить технологию выполнения измерений, под которой понимается совокупность основных приемов использования средств измерений и последовательность их реализации, требования к выбору средств измерений, числа измерений и их условий, способов обработки результатов. Все перечисленное составляет так называемую методику измерений. Это понятие широко используется в метрологической практике. Обычно под методикой измерений понимают установленную совокупность операций и правил, выполнение которых при измерении обеспечивает получение результатов измерений в соответствии с данным методом. В ряде случаев существуют нормативно-технические документы, регламентирующие конкретные методики измерений.
Результат измерений ‑ главная цель измерений. Результат любого измерения всегда отличается от истинного значения измеряемой величины, под которым подразумевают значение физической величины идеальным образом отражающее в качественном и количественном отношениях соответствующее свойство объекта. Поэтому для получения результата измерений необходимо оценить значение искомой величины в совокупности с оценкой ее отклонения от истинного значения. На практике для проведения этих оценок используются показания средств измерений и их характеристики. Исходя из этого, результатом измерений физической величины называется значение физической величины, полученное путем ее измерения.
Часто в полученный результат вносят поправки, что находит отражение в терминологии:
– неисправленный результат измерения - значение физической величины, полученное при помощи средств измерений до внесения поправок;
– исправленный результат измерения - значение физической величины, полученное при помощи средств измерений и уточненное путем внесения в него необходимых поправок.
Приведем еще несколько важных определений:
– сходимость результатов измерений - характеристика качества измерений, отражающая близость друг к другу результатов измерений одной и той же величины, выполняемых повторно одними и теми же средствами, одним и тем же методом в одинаковых условиях;
– воспроизводимость результатов измерений - характеристика качества измерений, отражающая близость друг к другу результатов измерений одной и той же величины, полученных в разных местах, разными методами и средствами, разными операторами, в разное время, но приведенных к одним и тем же условиям (температура, давление, влажность и др.);
– погрешность результата измерений - отклонение результата измерений от истинного значения измеряемой величины. Количественно погрешность характеризуют величиной 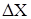 , равной разности между истинным
, равной разности между истинным 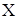 и измеренным
и измеренным 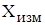 . значениями измеряемой величины
. значениями измеряемой величины
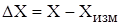 (2.2)
(2.2)
В зависимости от причины возникновения погрешности могут быть систематическими и случайными.
Систематическими называются погрешности, не изменяющиеся во времени или изменяющиеся во времени по известному закону. Основной отличительный признак систематических погрешностей состоит в том, что они могут быть предсказаны и благодаря этому практически полностью устранены введением соответствующих поправок.
Поправкой называется значение величины, одноименной с измеряемой, прибавляемое к полученному при измерении значению величины с целью исключения систематической погрешности.
Случайными называются погрешности, изменяющиеся непредсказуемым, случайным образом при повторных измерениях одной и той же величины. Основной отличительный признак случайных погрешностей состоит в том, что они (в отличие от систематических) легко обнаруживаются при повторных измерениях в виде некоторого разброса получаемых результатов. Описание случайных погрешностей может быть осуществлено только на основе теории вероятностей и математической статистики. Важно, что их влияние на результаты измерений в принципе неустранимо, а только может быть по необходимости уменьшено.
Точность результата измерений (кратко - точность измерений) - характеристика качества измерения, отражающая близость к нулю погрешности его результата. Количественно точность можно охарактеризовать величиной 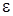 , обратной модулю относительной погрешности:
, обратной модулю относительной погрешности:
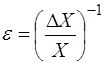 , (2.3)
, (2.3)
где DX- погрешность измерения, X - истинное значение измеряемой величины.
Правильность результата измерений – характеристика качества измерений, отражающая близость к нулю систематических погрешностей в их результатах;
Достоверность результата измерений – характеристика качества измерений, отражающая доверие к их результатам. Измерения делят на достоверные и недостоверные в зависимости от того известны или неизвестны вероятностные характеристики их отклонения от истинных значений измеряемых величин.