Трапецеидальные распределения

Общие сведения

Основные законы распределения

Использование на практике вероятностного подхода к оценке погрешностей результатов измерений прежде всего предполагает знание аналитической модели закона распределения рассматриваемой погрешности. Встречающиеся в метрологии распределения достаточно разнообразны. В качестве примера можно привести результаты исследований [4] 219 фактических распределений погрешностей, имеющих место при измерении электрических и неэлектрических величин разнообразными приборами. Установлено, что примерно 50% распределений принадлежат к классу экспоненциальных, 30% являются уплощенными, а остальные 20% — различными видами двухмодальных распределений.

Множество законов распределения случайных величин, используемых в метрологии, целесообразно классифицировать [4] следующим образом:

• трапецеидальные (плосковершинные) распределения;

• уплощеные (приблизительно плосковершинные) распределения;

• экспоненциальные распределения;

• семейство распределений Стьюдента;

• двухмодальные распределения.

К трапецеидальным распределениям относятся: равномерное, собственно трапецеидальное и треугольное (Симпсона). Равномерноe распределение (рис. 6.5,а) описывается уравнением

Трапецеидальное распределение (рис. 6.5, б) образуется как композиция двух равномерных распределений шириной а₁ и а₂, (рис. 6.2):

Рис. 6.5. Распределения: а — равномерное; б — трапецеидальное;

в — треугольное (Симпсона)

Треугольное (Симпсона) распределение (рис. 6.5, в) — это частный случай трапецеидального, для которого размеры исходных равномерных распределений одинаковы: а₁ = а₂ (см. рис. 6.2):

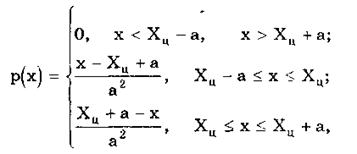
где Х_ц, а, b — параметры распределения.

Математическое ожидание всех трапецеидальных распределений Х_ц = (x₁ + х₂) / 2. Медианы из соображений симметрии равны МО. Равномерное и собственно трапецеидальное распределения моды не имеют, а мода треугольного равна 1/а.

Среднее квадратическое отклонение в зависимости от распределения определяется по формуле:

• равномерное ;

• трапецеидальное

• треугольное .

Из приведенных уравнений следует, что СКО трапецеидальных распределений возрастает в 1,41 раза с ростом параметра b от нуля (треугольное) до а (равномерное). Коэффициент асимметрии всех трапецеидальных распределений равен нулю.

Числовые параметры трапецеидальных распределений при различных отношениях ширины исходных равномерных распределений приведены в табл. 6.2.

Таблица 6.2

Значения параметров трапецеидальных распределений

b/а	a₂ /a₁ (см. рис. 6.2)	а/s	e	к	k
		1,732	1,8	0,745	1,73
2/3	1/5	2,037	1,9	0,728	1,83
1/2	1/3	2,191	2,016	0,704	1,94
1/3	1/2	2,324	2,184	0,677	2,00
		2,449	2,4	0,645	2,02

Равномерное распределение имеют погрешности: квантования в цифровых приборах, округления при расчетах, отсчета показаний стрелочного прибора, от трения в стрелочных приборах с креплением подвижной части на кернах или подпятниках, определения момента времени для каждого из концов временного интервала при измерении частоты и периода методом дискретного счета. Суммируясь между собой, эти погрешности образуют трапецеидальные распределения с различными отношениями сторон.