Основные законы распределения

Общие сведения. Использование на практике вероятностного подхода к оценке погрешностей результатов измерений, прежде всего, предполагает знание аналитической модели закона распределения рассматриваемой погрешности. Встречающиеся в метрологии распределения достаточно разнообразны. Множество законов распределения случайных величин, используемых в метрологии, целесообразно классифицировать следующим образом:
- трапецеидальные (плосковершинные) распределения;
- уплощеные (приблизительно плосковершинные) распределения;
- экспоненциальные распределения;
- семейство распределений Стьюдента;
- двухмодальные распределения.
Трапецеидальные распределенияК трапецеидальным распределениям относятся: равномерное, собственно трапецеидальное и треугольное (Симпсона). Равномерное распределение (рис. а) описывается уравнением

 

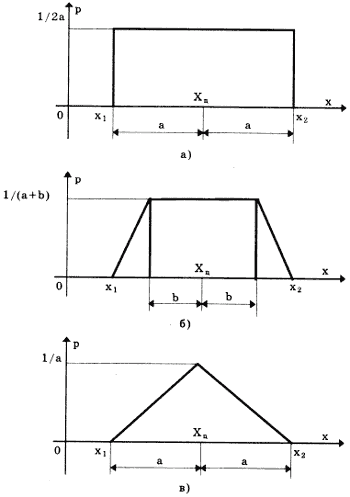
Трапецеидальное распределение (рис. б)

Треугольное (Симпсона) распределение (рис. в)

где Хц, a, b - параметры распределения.
Математическое ожидание всех трапецеидальных распределений Хц=(х₁+х₂)/2. Медианы из соображений симметрии равны МО. Равномерное и собственно трапецеидальное распределения моды не имеют, а мода треугольного равна 1/а.
Среднее квадратическое отклонение в зависимости от распределения определяется по формуле:
- равномерное
- трапецеидальное
- треугольное .
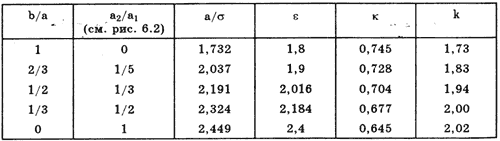
Из приведенных уравнений следует, что СКО трапецеидальных распределений возрастает в 1,41 раза с ростом параметра b от нуля (треугольное) до а (равномерное). Коэффициент асимметрии всех трапецеидальных распределений равен нулю. Числовые параметры трапецеидальных распределений при различных отношениях ширины исходных равномерных распределений приведены в табл.

Равномерное распределение имеют погрешности: квантования в цифровых приборах, округления при расчетах, отсчета показаний стрелочного прибора, от трения в стрелочных приборах с креплением подвижной части на кернах или подпятниках, определения момента времени для каждого из концов временного интервала при измерении частоты и периода методом дискретного счета. Суммируясь между собой, эти погрешности образуют трапецеидальные распределения с различными отношениями сторон.
Экспоненциальные распределения Экспоненциальные распределения описываются формулой 1

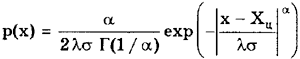
где ; - СКО; - некоторая характерная для данного распределения константа; Хц - координата центра; Г(х) - гамма-функция. В нормированном виде, т.е. при Хц = О и = 1,

где А() - нормирующий множитель распределения.
Интегральная функция нормированного экспоненциального распределения описывается выражением

Интеграл, входящий в эту формулу, выражается через элементарные функции только при = 1/n, n = 1; 2; 3; ... При = n = 2; 3; 4; ... он может быть рассчитан по приближенным формулам.
Эксцесс и энтропийный коэффициент экспоненциальных распределений соответственно определяются по формулам:

Анализ приведенных выражений показывает, что константа а однозначно определяет вид и все параметры распределений. При < 1 распределение имеет очень пологие спады и по форме близко к распределению Коши. При = 1 получается распределение Лапласа , при = 2 - нормальное распределение или распределение Гаусса. При > 2 распределения, описываемые формулой 1, близки по свойствам к трапецеидальным. При очень больших значениях а формула (1) описывает практически равномерное распределение. В табл. приведены параметры некоторых из экспоненциальных распределений.

Вид экспоненциальных распределений при различных значениях показателя приведен на (рис).