Безынерционное звено.
?????????????????????????????????????????????????????????????????
§1.17. Логарифмические частотные характеристики (ЛАЧХ).
Для инженерных расчетов более удобно использовать не частотные, а логарифмические частотные характеристики. Они представляют собой построение АЧХ и ФЧХ в логарифмическом масштабе. Простота использования таких характеристик определяется тем, что для получения результирующих характеристик можно графически складывать частотные характеристики, а для типовых динамических звеньев можно элементарно просто строить асимптотические ЛАЧХ, т.е. характеристики в виде ломанных линий из прямолинейных отрезков, к которым асимптотически приближаются действительные ЛАЧХ, рассматриваемых динамических звеньев.
По оси абсцисс в таких координатных сетках откладывают частоту в логарифмическом масштабе. За единицу принимается декада (при десятикратной разнице в частотах) или октава (двукратной разнице в частотах). Декада и октава – это акустические единицы.
По оси ординат в равновесном масштабе откладывают логарифмическую амплитуду.
 1.45
1.45
Единица измерения L(w) принят дБ. Белл – логарифмическая единица, соответствующая десятикратному увеличению мощности. При построении логарифмических характеристик по оси ординат откладывают логарифмическую амплитуду в дБ и аргумент j в градусах или радианах, а по оси абсцисс lg(w) в декадах.
§1.18. Типовые динамические звенья.
Элементы и САУ, описываемые динамическими уравнениями могут быть представлены элементарными звеньями. Число типов элементарных звеньев ограничены и по разным классификационным признакам они объединены в группу:
1. Простые звенья:
1) безынерционное звено (усилительное или пропорциональное звено).
2) интегрирующее звено.
3) дифференцирующее звено.
2. Звенья первого и второго порядка.
1) апериодическое звено первого порядка.
2) колебательное звено.
3) консервативное звено.
4) апериодическое звено второго порядка.
3. Трансцендентные звенья.
1) звено транспортного запаздывания
2) звено чистого запаздывания
Изучение типовых звеньев будем проводить в следующем порядке:
1. Определение и динамическое уравнение звена.
2. Передаточная функция.
3. Примеры звеньев.
4. Переходная функция и функция веса.
5. Переходная и переходная импульсная характеристики.
6. Аналитические выражения АЧХ, ФЧХ, ЛАЧХ и АФЧХ.
7. Изображение ЛЧХ, АФЧХ, ФЧХ, ЛАЧХ.
Это звено относится к группе простейших звеньев, выходная величена в которых пропорциональна входной величине, ее интегралу или производной.
Безынерционным или пропорциональным называется звено, которое как и в переходном, так и в установившемся режиме описывается уравнением:
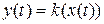 1.46
1.46
где к – коэффициент передачи или пропорциональности.
Предполагается, что реакция звена на входное воздействие происходит мгновенно без всякой инерции. Устройство считается безинерционным, если его инерционность значительно меньше (на несколько порядков) инерционности других устройств, входящих в систему.
Примеры безынерционных звеньев:

усилительделитель напряженияредуктор
Передаточная функция этого звена:
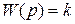 1.47
1.47
Переходная функция:
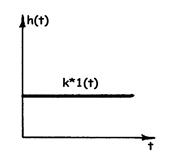 |
 1.48
1.48
Весовая функция:
 |
 1.49
1.49
Частотные характеристики:
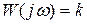 1.50
1.50
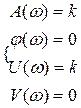 1.51
1.51
Вид частотных характеристик:
АФХ АЧХ ФЧХ
 | |||
 | |||
φ(ω)=0
Логарифмические частотные характеристики:
 1.52
1.52
Вид логарифмических характеристик:
