Математическое описание САР и их элементов
Классификация систем автоматического регулирования (САР).
В зависимости от основной цели задачи управления САР классифицируются следующим образом: системы стабилизации, система программного управления, следящие системы.
В системах стабилизации рабочий параметр объекта (регулируемая величина) поддерживается постоянным во времени при постоянном задании.
В системах программного управления рабочий параметр объекта изменяется во времени по заранее известному закону, в соответствии с которым изменяется задание.
В следящих системах рабочий параметр объекта изменяется во времени по заранее неизвестному закону, который определяется каким-то внешним независимым процессом.
В зависимости от характера действия различных элементов, входящих в систему регулирования, различают системы непрерывного и дискретного действия.
Непрерывная система автоматического регулирования состоит только из звеньев непрерывного действия, выходная величина которых изменяется при плавном изменении входной величины.
Дискретная система содержит хотя бы одно звено дискретного действия, выходная величина которого изменяется скачками (дискретами) при плавном изменении входной величины. Дискретныесистемы в свою очередь, могут быть релейными, импульсными или цифровыми. Вследствие бурного развития микроэлектроники широкое распространение получили цифровые системы управления, обладающие, прежде всего высокой точностью.
Важным свойством также является поведение параметров системы во времени.
Если в период эксплуатации параметры являются неизменными, то система считается стационарной, в противном случае - нестационарной. Кроме того, особо выделяются системы с распределенными параметрами, т.е. такие системы, которые содержат распределенные в пространстве элементы, например, длинные электрические линии и т.д.
Указанные выше свойства систем определяют вид математического описания протекающих процессов. При этом необходимо иметь ввиду, что большинство систем обладают свойством инерционности. Поэтому в системах можно наблюдать переходной процесс и установившийся режим. Наиболее приемлемым способом математического описания в этом случае являются дифференциальные уравнения (для непрерывных систем) или разностные уравнения (для дискретных систем). Вид дифференциального уравнения зависит от основных свойств, которыми обладает САР. В простейших случаях это линейные дифференциальные уравнения с постоянными коэффициентами. По способу математического описания системы регулирования делятся на линейные и нелинейные.
В зависимости от характера внешних воздействий (задающего и возмущающего) различают детерминированные и стохастические системы. В детерминированных САР внешние воздействия имеют вид постоянных функций времени. В стохастических системах внешние воздействия имеют вид случайных функций. В дальнейшем будут рассматриваться только детерминированные системы.
По свойствам ошибки (отклонения) в установившемся режиме различают статические и астатические системы. Система, в которой величина установившейся ошибки зависит то величины возмущения при постоянном задании, называется статической по возмущению. Если установившаяся ошибка не зависит от величины возмущения, то система является астатической 1-ого порядка. Если установившаяся ошибка не зависит от первой производной возмущающего воздействия, то система является астатической 2-го порядка.
По числу контуров прохождения сигналов АСР делят на: одноконтурные(если она состоит из одного контура регулирования) и многоконтурные. Многоконтурные АСР могут применяться и для регулирования одной величины с целью повышения качества переходного процесса.
По числу регулируемых величин различают одномерные и многомерные системы автоматического регулирования. В свою очередь многомерные САР делятся на системы несвязанного и связанного регулирования. Характерным для первых является то, что регуляторы в них непосредственной связи между собой не имеют и взаимодействуют только через объект регулирования. В системах связанного регулирования регуляторы различных параметров одного и того же объекта имеют непосредственные взаимные связи помимо связей через объект регулирования.
Наряду с рассмотренными системами автоматического регулирования применяются также экстремальные системы.
Оптимальный режим работы объекта характеризуется экстремальным (максимальным или минимальным) значением показателя эффективности процесса, протекающего в объекте. Таким показателем может быть либо технологическая величина, либо одна из экономических характеристик. Вследствие влияния возмущений оптимальный режим работы объектов нарушается. Системы стабилизации не способны скомпенсировать такие отклонения. Для отыскания оптимального режима служат экстремальные системы. Эта задача решается автоматическим поиском таких значений управляющих воздействий, которые соответствуют экстремальному значению показателя эффективности процесса. Системы, осуществляющие автоматический поиск нескольких управляющих величин объекта с целью обеспечения экстремального значения показателя эффективности протекающего в нем процесса, называются оптимальными. На практике же оптимизируемая величина объекта часто зависит не от нескольких, а от одной управляющей величины; такие оптимальные системы называют экстремальными системами.
Рассмотренные выше разновидности не исчерпывают всего многообразия САР.
Целью рассмотрения систем автоматического регулирования может быть решение одной из двух задач - задачи анализа или синтеза системы. В первом случае имеется система, известны ее параметры, требуется определить свойства системы, например качество переходных процессов, устойчивость, точность. Во втором случае, наоборот, задаются свойства системы и необходимо создать систему, удовлетворяющую этим свойствам. Эта задача, как правило, неоднозначна и много сложнее задачи анализа.
В самом общем виде порядок исследования системы регулирования включает математическое описание системы, исследование установившихся и переходных режимов.
Под математическим описанием понимают дифференциальное уравнение или систему дифференциальных уравнений высокого порядка, описывающую систему регулирования.
Для упрощения математического описания систему разбивают на отдельные элементы – звенья, каждые из которых выполняют свои самостоятельные функции. Они описываются либо аналитически в виде дифференциальных уравнений не выше 2-го порядка, либо графически в виде характеристик, связывающих входные и выходные величины звена. Главное требование, которому должны удовлетворять звенья системы регулирования, - это требование направленности действия. Звеном направленного действия называется звено, которое передает воздействие только в одном направлении — со входа на выход, так что при последовательном соединении X звеньев изменение состояния последующего звена не влияет на состояние предшествующего звена.
В результате при разбивке системы на звенья направленного действия математическое описание каждого звена может быть составлено без учета его связей с другими звеньями. При этом математическое описание всей системы регулирования может быть получено как совокупность дифференциальных уравнений или характеристик отдельных звеньев, дополненных уравнениями связи между звеньями.
Свойства систем автоматического регулирования определяются статическими и динамическими характеристиками звеньев, входящих в систему, причем объект управления рассматривается как составное звено системы управления.
Статической характеристикой элемента (технического устройства) называется зависимость его выходной величины от входной в равновесных состояниях, то есть:

Статическая характеристика может быть представлена уравнением, графиком или таблицей. При графическом изображении статической характеристики по оси абсцисс откладывают значения входной величины  , а по оси ординат – значения выходной величины
, а по оси ординат – значения выходной величины  .
.
Статическая характеристика называется линейной, если зависимость между  и
и  линейна (графически она представляет собой прямую линию). Элемент с такой характеристикой также называется линейным.
линейна (графически она представляет собой прямую линию). Элемент с такой характеристикой также называется линейным.
Если характеристика описывается нелинейным уравнением или системой уравнений, а ее график есть кривая или ломаная линия, то такая характеристика называется нелинейной, а элемент – нелинейным. Возможные характеристики линейного и нелинейного элементов показаны на рис.6.
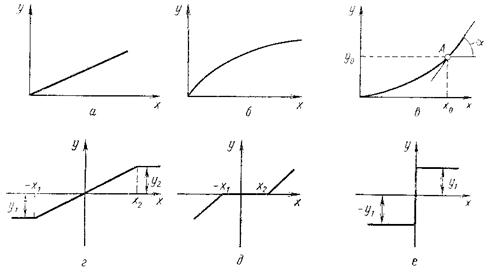
Рис. 6 – Статические характеристики элементов:
а – линейная, б, в, г, д, е – нелинейные.
Уравнение линейной статической характеристики имеет вид:

где  - коэффициент пропорциональности, называемый коэффициентом усиления.
- коэффициент пропорциональности, называемый коэффициентом усиления.
Для нелинейных элементов математическая запись статической характеристики может быть различной в зависимости от вида нелинейности.
Большинство элементов, входящих в САР, в большей или меньшей степени нелинейны.
Учитывая, что расчеты САР производятся для сравнительно небольших отклонений переменных величин от их базовых значений ( ,
,  ), поэтому уравнения записываются не в абсолютных значениях переменных, а в их абсолютных отклонениях:
), поэтому уравнения записываются не в абсолютных значениях переменных, а в их абсолютных отклонениях:

Нелинейные элементы с плавно изменяющимися характеристиками можно рассматривать как имеющие линейную статическую характеристику. При этом линеаризацию статической характеристики можно производить не на всем диапазоне значений входных и выходных величин, а на небольшом участке в окрестности точки, соответствующей равновесному состоянию.
На рис.6. (в) небольшой участок нелинейной характеристики около точки А (базовых значениях  и
и  ) можно считать линейным. Он совпадает с касательной, проведенной к кривой в этой точке. Коэффициент усиления линейного участка характеристики определяется здесь как тангенс угла наклона
) можно считать линейным. Он совпадает с касательной, проведенной к кривой в этой точке. Коэффициент усиления линейного участка характеристики определяется здесь как тангенс угла наклона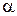 касательной к оси абсцисс:
касательной к оси абсцисс:
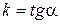
В дальнейшем мы будем рассматривать элементы, характеристики которых линейны или могут быть линеаризованы с допустимой степенью точности.
Системы регулирования, состоящие из таких элементов, называются линейными (или линеаризованными).
Так как САР являются динамическими системами, знания одних только статических свойств элементов САР недостаточно. Необходимо знать динамические свойства элементов САР, оцениваемые динамическими характеристиками.
Динамической характеристикой элемента называют зависимость изменения во времени выходной величины  от изменения входной
от изменения входной  в переходном режиме, т.е. при переходе из одного состояния в другое; характер изменения входной величины может быть разным.
в переходном режиме, т.е. при переходе из одного состояния в другое; характер изменения входной величины может быть разным.
Динамические свойства элементов (и САР в целом) могут быть представлены дифференциальными уравнениями, с помощью которых описываются переходные процессы в элементах. Поэтому задача определения динамической характеристики того или иного элемента системы сводится к составлению его дифференциального уравнения на основании знания принципа действия и физических законов, положенных в основу работы элемента.
Рассмотрим схему звена, изображенного на рис.7. Описанием звена служит дифференциальное уравнение, связывающее выходную величину Y и входную X. Пусть, например, связь между X и Y выражается уравнением 2-го порядка
 (1)
(1)
В теории автоматического регулирования приняты определенные формы записи линейных дифференциальных уравнений звеньев, которые основаны на введении символа дифференцирования по времени — оператора  , т. е.
, т. е. , где
, где 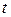 независимая переменная. Метод математического анализа получил название операционный (
независимая переменная. Метод математического анализа получил название операционный ( - оператор). В основу метода положен известный метод интегральных преобразований Лапласа.
- оператор). В основу метода положен известный метод интегральных преобразований Лапласа.
Тогда можно записать
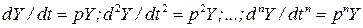 (2)
(2)
 Рис 7. Схема звена САР
Рис 7. Схема звена САР
Исходное дифференциальное уравнение представим в виде
 (3)
(3)
или
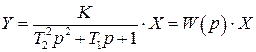 (4)
(4)
где
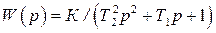 (5)
(5)
 называется передаточной функцией звена. Мы будем рассматривать ее как удобный способ записи дифференциальных уравнений.
называется передаточной функцией звена. Мы будем рассматривать ее как удобный способ записи дифференциальных уравнений.
Постоянные коэффициенты 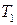 и
и  называют постоянными времени, а
называют постоянными времени, а  — коэффициентом усиления (передачи) звена.
— коэффициентом усиления (передачи) звена.
Помимо уравнений динамические свойства линейных звеньев могут быть описаны графическими характеристиками двух типов: переходными и частотными.
Переходная, или временная характеристика f(t) представляет собой график изменения во времени выходной величины звена, вызванного подачей на его вход единичного ступенчатого воздействия.

Входной сигнал, имеющий вид единичного скачка, приведен на рис.8.

Рис.8. — Единичный скачок
Если на вход звена подается гармоническое возмущение, то исследование динамики осуществляется частотными методами с использованием частотных характеристик основных типов: амплитудно-частотной (АЧХ), фазочастотной (ФЧХ), амплитудно-фазовой (АФХ), вещественной частотной (ВЧ), и мнимой частотной (МЧ).
Частотные характеристики описывают установившиеся вынужденные колебания на выходе звена при подаче на его вход гармонического воздействия:

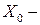 амплитуда;
амплитуда;  - угловая частота; Т- период колебаний. В этом случае на выходе звена будем иметь
- угловая частота; Т- период колебаний. В этом случае на выходе звена будем иметь
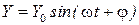
где 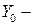 амплитуда установившихся выходных колебаний;
амплитуда установившихся выходных колебаний;  фазовый сдвиг между входными и выходными колебаниями (рис 9 ).
фазовый сдвиг между входными и выходными колебаниями (рис 9 ).
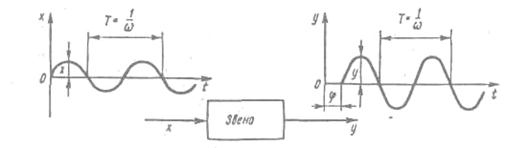
Рис 9. Входная и выходная величины при гармонических возмущениях звена
При фиксированной амплитуде входных колебаний амплитуда  и фаза
и фаза  зависят от частоты
зависят от частоты  . Если постепенно увеличивать от нуля частоту колебаний, определяя установившиеся значения
. Если постепенно увеличивать от нуля частоту колебаний, определяя установившиеся значения  и
и  для разных частот при фиксированном значении
для разных частот при фиксированном значении  , то можно получить зависимости
, то можно получить зависимости  и
и 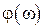 , которые называются:
, которые называются:
 - амплитудной частотной характеристикой;
- амплитудной частотной характеристикой;
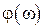 - фазовой частотной характеристикой звена.
- фазовой частотной характеристикой звена.
Запишем гармонические сигналы на входе и выходе звена в комплексной форме:

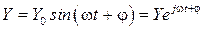
где
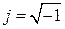 ,
,
тогда
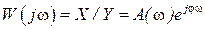
Таким образом, подставляя в выражение для передаточной функции  вместо
вместо  комплексную величину
комплексную величину  , мы получаем зависимость между передаточной функцией и частотными характеристиками звена. При этом комплексная величина
, мы получаем зависимость между передаточной функцией и частотными характеристиками звена. При этом комплексная величина 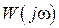 есть функция частоты и называется амплитудно-фазовой характеристикой звена.
есть функция частоты и называется амплитудно-фазовой характеристикой звена.
При построении 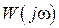 в прямоугольной системе координат – комплексной плоскости – получаем годограф амплитудно-фазовой характеристики, где частота
в прямоугольной системе координат – комплексной плоскости – получаем годограф амплитудно-фазовой характеристики, где частота входит как параметр. Примерный вид годографа показан на рис.10. Каждой точке такого годографа соответствует определенная частота
входит как параметр. Примерный вид годографа показан на рис.10. Каждой точке такого годографа соответствует определенная частота 

Рис 10. Амплитудно-фазовая характеристика
Следует отметить, что для линейных звеньев существует однозначная связь между дифференциальным уравнением, временными и частотными характеристиками звена. Это означает, что, зная дифференциальное уравнение (или передаточную функцию) звена, можно построить переходную или амплитудно-фазовую характеристику звена и наоборот.