По характеру замыкания звеньев кинематические пары делятся на замкнутые геомет­рически и замкнутые не геометрически: силой или кинематической цепью.

Классификация кинематических пар

 

1.По характеру касания звеньев кинематические пары делятся на высшие и низшие.

Низшими кинематическими парами называются такие пары, звенья которых со­прикасаются по поверхностям.

Высшими кинематическими парами называются такие пары, звенья которых со­прикасаются по линии или в точке. Этот признак деления кинематических пар предполагает, что соприкасающиеся звенья (тела), образующие кинематические пары, абсолютно твёрдые. Если соприкасаю­щиеся тела не обладают этим свойством, то касание их по линии или в точке превра­щается в касание по некоторой поверхности.

 

 

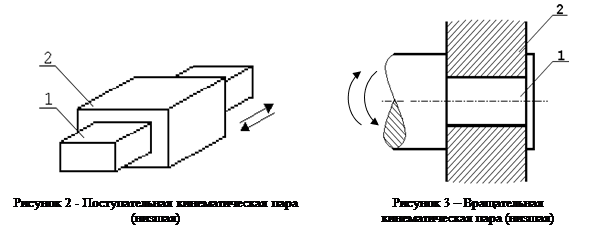Примеры низших кинематических пар приведены на рисунках 2 и 3. Ползун 1 движется в направляющей 2 (рисунок 2). Касание звеньев 1 и 2 происходит по плоско­стям. Это поступательная кинематическая пара. На рисунке 3 показана вращательная кинематическая пара. Звено 1 может совершать вращательное движение по отношению к звену 2. Касание звеньев здесь происходит по цилиндрической поверхности. Примером высших кинематических пар могут быть цилиндр на плоскости – касание звеньев про­исходит по линии – образующей цилиндра (рисунок 4); и шар на плоскости – касание звеньев происходит в точке (рисунок 5).

2.По характеру относительного движения звеньев кинематические пары делятся на плоские и пространственные.

Плоскими называются такие кинематические пары, относительное движение звеньев которых плоское.

Относительное движение – движение одного звена при мысленно неподвижном втором. Плоским движением тела называется такое движение, при котором все точки тела движутся параллельно некоторой неподвижной плоскости –плоскости параллелизма.

Кинематическая пара называется плоской если относительное движение звеньев:

плоско – параллельное – параллельно некоторой неподвижной плоскости;

поступательное – любая прямая тела движется параллельно некоторой прямой на неподвижной плоскости;

вращательное – вращение тела вокруг неподвижной оси.

Кинематическая пара называется пространственной, если относительное дви­жение её звеньев не плоское.

На рисунках 6-10 приведены примеры плоских кинематических пар. На рисунке 6 изображена плоская кинематическая пара при одном неподвижном звене 2, а на ри­сунке 7 – поступательная плоская пара с двумя подвижными звеньями.

Деление кинематических пар на плоские и про­странственные диктуется характером относительного движения их звеньев, которое в этих парах плоское.

На рисунке 8 показана вращательная кинематическая пара плоская – шарнир­ное соединение двух звеньев (рычагов). Вращательной кинематической парой плоской является также и колесо со станиной (рисунок 9).

На рисунке 10 показана плоско – параллельная кинематическая пара (колесо-рельс). Качение окружности по прямой – плоско–параллельное движение.

На рисунке 11 приведен пример пространственной кинематической пары – ша­ровой шарнир. Шар в шаровом гнезде может совершать вращение вокруг любой из 3^х осей X, Y, Z.

На рисунке 12 показана также пространственная кинематическая пара – вин­товая пара. Любая точка гайки при мысленно закреплённом винте совершает простран­ственное движение. Траектория любой точки гайки – винтовая линия.

Соединение звеньев в кинематические пары может быть осуществлено по-раз­ному. При геометрическом замыкании звенья конструктивно соединены в кинематические пары. В качестве примера можно рассмотреть колесо со станиной (рисунок 9) или шар­нирное соединение двух рычагов (рисунок 8).

При силовом замыкании кинематическая пара существует за счёт сил веса или сил пружин. Например шар на плоскости (рисунок 5) или колесо рельс (рисунок 10).При замыкании кинематической цепью пара существует за счёт других кинема­тических пар в кинематической цепи, которые не позволяют нарушить контакт звеньев, образующих кинематическую пару. Например кинематическая пара, образованная зацеп­лением двух зубчатых колёс 1, 2 (рисунок 1).

4.

По характеру повторяемости траекторий точек элементов кинематических пар пары делятся на обратимые и необратимые.

О

Обратимыми называются такие кинематические пары, траектории точек элемен­тов кинематических пар которых повторяются. Например во вращательной паре (рисунок 13) при движении звена 1 по отношению к звену 2 траектория точки А, лежащей на поверхности соприкосновения звеньев и принадлежащей звену 1, – окруж­ность. При мысленно закрепленном звене 1 траектория точки А, принадлежащей звену 2, в относительном движении, также окружность радиуса ОА.

Необратимыми называются такие кинематические пары, траектории точек эле­ментов которых в относительном движении не повторяются. Примером является плоская кинематическая пара колесо – рельс. При обкатывании колеса по направляющей точка А (рисунок 14) описывает циклоиду, а при обкатывании прямой по окружности – эволь­венту.

5.По числу потерянных степеней свободы в относительном движении или по числу ус­ловий связей кинематические пары делятся на 5 классов (или по степеням подвижности – 1^но, 2^х, 3^х, 4^х и 5^ти подвижные кинематические пары).

Класс пары – это число условий связей, накладываемых парой на относитель­ное движение звеньев, или число потерянных степеней свободы в относительном движе­нии звеньев.

Тело, свободно перемещающееся в пространстве, имеет 6 степеней свободы: движение вдоль осей X, Y, Z и вращение вокруг этих осей. Степень свободы – обоб­щённая координата – это число независимых параметров, которыми определяется поло­жение тела в пространстве или его движение.

Соединяя звенья в кинематические пары мы тем самым лишаем их одной или нескольких степеней свободы. В зависимости от числа потерянных степеней свободы в относительном движении звеньев, связанных в кинематические пары, пространственные пары делятся на 5 классов. Для иллюстрации классификации кинематических пар соста­вим таблицу, включающую примеры всех 5 классов пространственных пар (таблица 1).