Затухающие электромагнитные

Рис. 11.1

 

равную , где Так как R ≈ 0, то полная энергия и на нагревание не расходуется. Поэтому в момент времени (рис. 11.1,б), когда конденсатор полностью разрядится, энергия электрического поля обращается в ноль, а энергия магнитного поля (следовательно, и ток) достигает наибольшего значения. Начиная с этого момента, ток в контуре начинает убывать (начинает ослабевать магнитное поле катушки) и индуцируется ток, который течет согласно правилу Ленца в том же направлении, что и ток разрядки конденсатора. Конденсатор начинает перезаряжаться, возникает электрическое

поле, стремящееся ослабить ток, который в конце концов обращается в ноль, а заряд на обкладках конденсатора достигает максимума (рис. 11.1,в). Далее те же процессы начнут протекать в обратном направлении (рис. 11.1,г) и система к моменту времени t = T придет в первоначальное состояние (см. рис. 11.1,а). Затем начнется повторение цикла «разрядка – зарядка» конденсатора. Если бы не было потерь энергии, то в контуре совершались бы периодические незатухающие колебания, сопровождающиеся взаимными превращениями энергии электрического и магнитного полей.

Согласно закону Ома для контура можно записать IR + U_c = ε_s, где IR – напряжение на резисторе; – напряжение на конденсаторе; 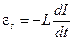– ЭДС самоиндукции (единственная ЭДС, действующая в контуре). В итоге имеем Учитывая, что ; , получим дифференциальное уравнение колебаний заряда Q в контуре

(11.1)

В данном контуре нет внешних ЭДС и колебания являются свободными. Если R = 0, то свободные электромагнитные колебания в контуре являются гармоническими и дифференциальное уравнение этих колебаний имеет вид

(11.2)

Следовательно, можно сделать вывод, что рассматриваемый контур является гармоническим осциллятором и в нем заряд Q совершает гармонические колебания по закону

j), (11.3)

где Q_m – амплитуда колебаний заряда конденсатора с циклической частотой w₀, называемой собственной частотой колебаний контура

(11.4)

и периодом

. (11.5)

Выражение (11.5) называют формулой Томсона[1], в честь впервые получившего ее ученого.

Сила тока в колебательном контуре и напряжение на конденсаторе соответственно равны:

j) = I_m cos (w₀t + j + ; (11.6)

cos (w₀t + j) = U_m cos (w₀t + j). (11.7)

Из уравнений (11.3), (11.6) и (11.7) следует, что в идеализированном контуре колебание тока опережает на фазе колебания заряда и напряжения на .