Задача о максимальном потоке

Рассмотрим задачу определения максимального потока между выделенными узлами связной сети. Каждая дуга сети обладает пропускными способностями в обоих направлениях, которые определяют максимальное количество потока, проходящего по данной дуге. Ориентированная (односторонняя) дуга соответствует нулевой пропускной способности в запрещенном направлении.

Пропускную способность C_ij сети можно представить в матричной форме.

Алгоритм решения:

Шаг1:
Найти цель, соединяющую источник S и сток t , по которой поток принимает положительное значение. В направлении S→t. Если такой цели не существует, перейти к шагу 3. В противном случае перейти к шагу 2.

Шаг 2:

Пусть 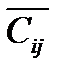( 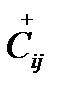) – пропускные способности дуг цепи (S,t) в направлении S→t(t→ S).

ϴ= min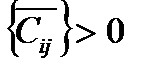

Матрицу пропускных способностей C=[C_ij] изменить следующим образом:

а) вычесть ϴ из всех ;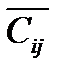

б) прибавить ϴ ко всем .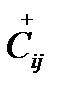

Заменить текущую матрицу С на вновь полученную и перейти к шагу 1. Операция (а) дает возможность использовать остатки пропускных способностей дуг выбранной цепи в направлении S→t.

Операция (б) восстанавливает исходные пропускные способности сети, т.к. уменьшение пропускной способности дуги в одном направлении можно рассматривать как увеличение ее пропускной способности в противоположном направлении.

Шаг 3:

Найти максимальный поток в сети.

Пусть C=[C_ij]- исходная матрица пропускных способностей.

C*=[C*_ij] – последняя матрица, получившаяся в результате модификации исходной матрицы (шаг 1 и 2) .

Оптимальный поток Х=[x_ij] в дугах задается так:

X_ij =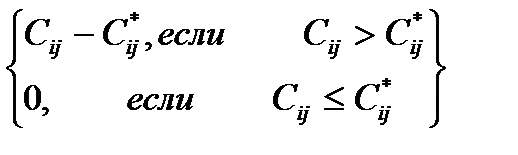

Максимальный поток из S в t равен:

 

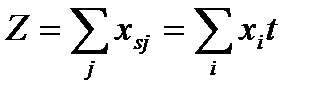
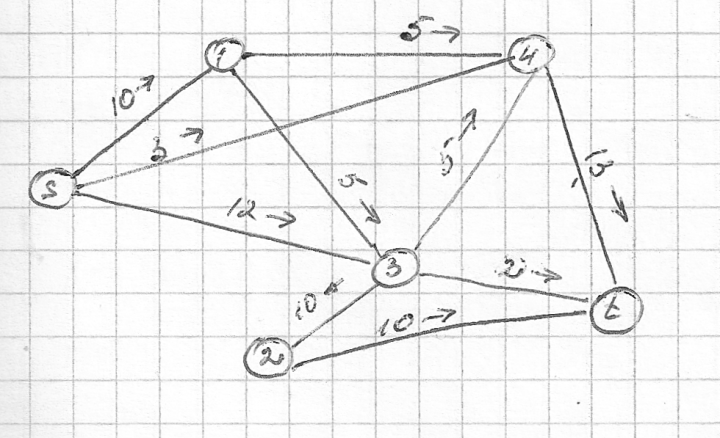
Пример: определить максимальный поток в графе

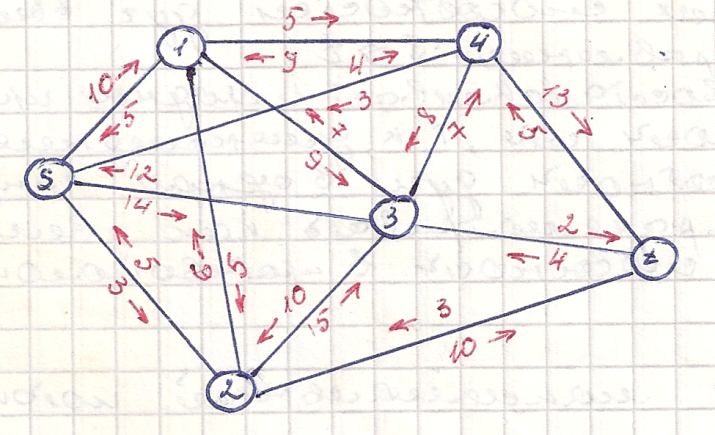
S 1 2 3 4 t

C =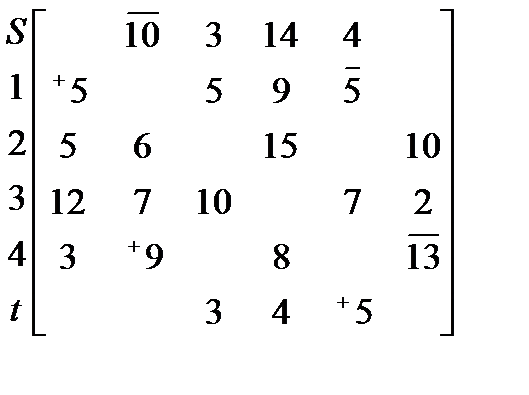

I итерация

Шаг 1.

В качестве исходной цепи выберем S→1→4→t. Тогда ячейки (S,1),(1,4),(4,t) помечаем знаком (−), а ячейки (1,S),(4,1),(t,4) помечаем знаком (+).

Максимальный поток для этой цепи равен

ϴ= min{C_s1 , C₁₄ , C_4t}=min{10, 5 , 13}=5

Можно выбрать различные исходные цепи. Хороший выбор должен давать наибольшее значение ϴ. Но может возникнуть много вариантов таких цепей. При программировании цепь удобно определять непосредственно из матрицы С, начиная с первой строки S-строки и выбирая следующий узел среди тех, которые соединены с S положительным потоком. Далее рассматривается строка, соответствующая выбранному узлу, и выбирается следующий узел, соединенный с предыдущим положительной дугой. Процесс продолжается до тех пор , пока не будет достигнут узел t.

Корректируем матрицу С, вычитая ϴ= 5 из всех элементов, помеченных (−), и складывая со всеми элементами, имеющими знак (+). Получаем новую матрицу.

Аналогичные действия производим и на последующих итерациях.

 

II итерация

S 1 2 3 4 t

Выберем цепь (S→3→ 2→ t)

ϴ= min{14, 20, 10}=10 Скорректируем матрицу С

III итерация.

S 1 2 3 4 t

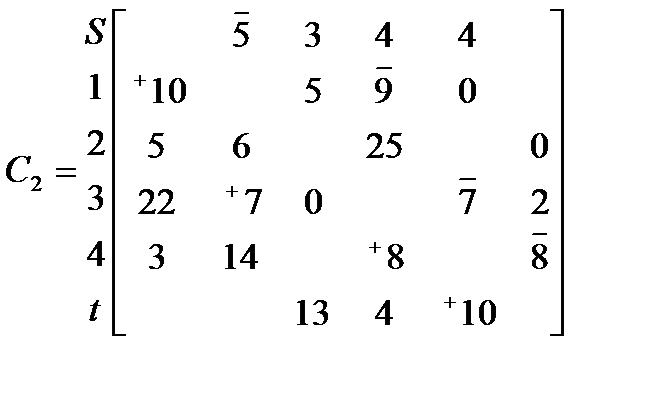
Выберем цепь (S→1→3→4→t)

ϴ= min{5, 9, 7, 8}=5 Скорректируем матрицу С

IV итерация

S 1 2 3 4 t

Выберем цепь (S→4→t)

ϴ= min{4, 3}=3 Скорректируем матрицу С

 

V итерация

S 1 2 3 4 t

Выберем цепь (S→3→t)

ϴ= min{4, 2}=2 Скорректируем матрицу С

VI итерация

S 1 2 3 4 t

Между S и t нельзя построить цепь ,т.к все элементы в столбце t равны нулю. Таким образом получим матрицу С*

Построим матрицу Х. Отрицательные элементы в матрице заменим нулями.

S 1 2 3 4 t

Х=

∑ ϴ= 5+10+5+3+2=25

 

Графически решение представлено графом: