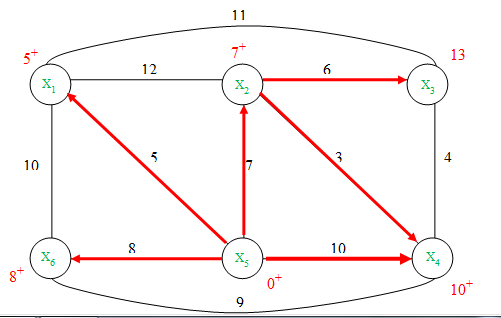
Четвёртая итерация
Шаг 2. Определим соответствие Г(р) и обновим временные пометки вершин, входящих в это соответствие.
Г(p) = Г(X6) = {X1, X4, X5}
Так как вершины X1 и X5 имеет постоянные пометки, то их не рассматриваем.
l(X4) = min{l(X4); l(p) + c(p(X4))} = min {10, 8+9} = 10
Шаг 3. Выберем минимальную пометку из всех временных, сделаем ее постоянной и присвоим «р» номер, соответствующий этой вершине
min{13, 10} = 10 => l(X4*)= 5+
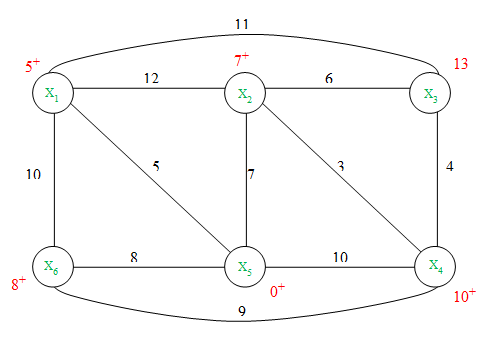
Так как вершина X3 единственная вершина с временной пометкой, то на этой итерации считаем l(X3*)= 13
Так как все вершины имеют постоянные пометки, то итерационный процесс закончен. Пометки вершин дают точную длину кратчайшего пути от исходной вершины X5 ко всем вершинам.
Определим сами кратчайшие пути в графе. Для этого используется соотношение :
l(Xi*)+c(Xi*,Xi)= l(Xi),
Пусть Хi = X1, ей предшествуют вершины X2; X3; X5; X6
l(X2) + c(X2, X1) = 7 + 12 = 19 ≠ l(X1)
l(X3) + c(X3, X1) = 13 + 11 = 24 ≠ l(X1)
l(X5) + c(X5, X1) = 0 + 5 = 5 = l(X1)
l(X6) + c(X6, X1) = 8 + 10 = 18 ≠ l(X1)
Следовательно, дуга (X5, X1) входит в кратчайший путь
1)Пусть Хi = X2, ей предшествуют вершины X1; X3; X4; X5
l(X1) + c(X1, X2) = 5 + 12 = 17 ≠ l(X2)
l(X3) + c(X3, X2) = 13 + 6 = 19 ≠ l(X2)
l(X4) + c(X4, X2) = 10 + 3 = 13 ≠ l(X2)
l(X5) + c(X5, X2) = 0 + 7 = 7 = l(X2)
Следовательно, дуга (X5, X2) входит в кратчайший путь
2)Пусть Хi = X3, ей предшествуют вершины X1; X2; X4
l(X1) + c(X1, X3) = 5 + 11 = 16 ≠ l(X3)
l(X2) + c(X2, X3) = 7 + 6 = 13 = l(X3)
l(X4) + c(X4, X3) = 10 + 4 = 14 ≠ l(X3)
Следовательно, дуга (X2, X3) входит в кратчайший путь
3)Пусть Хi = X4, ей предшествуют вершины X2; X3; X5; X6
l(X2) + c(X2, X4) = 7 + 3 = 10 = l(X4)
l(X3) + c(X3, X4) = 13 + 4 = 17 ≠ l(X4)
l(X5) + c(X5, X4) = 0 + 10 = 10 = l(X4)
l(X6) + c(X6, X4) = 8 + 9 = 17 ≠ l(X4)
Следовательно, дуги (X2, X4) и (X5, X4) входят в кратчайший путь
4)Пусть Хi = X6, ей предшествуют вершины X1; X4; X5
l(X1) + c(X1, X6) = 5 + 10 = 15 ≠ l(X6)
l(X4) + c(X4, X6) = 10 + 9 = 19 ≠ l(X6)
l(X5) + c(X5, X6) = 0 + 8 = 8 = l(X6)
Следовательно, дуга (X5, X6) входит в кратчайший путь
Таким образом, в кратчайший путь от вершины X5 ко всем вершинам входят дуги:
- к вершине X1: (X5, X1) вес пути = 5;
- к вершине X2: (X5, X2) вес пути = 7;
- к вершине X3: (X5, X2) (X2, X3) вес пути = 13;
- к вершине X4: (X5, X2) (X2, X4) вес пути = 10;
или (X5, X4) вес пути = 10;
- к вершине X6: (X5, X6) вес пути = 8;
На графе все кратчайшие пути выделены красными линиями