ДОМАШНЯЯ КОНТРОЛЬНАЯ РАБОТА ПО ДИСЦИПЛИНЕ «ЛОГИСТИКА»
Вариант №2 (Первая буква фамилии студентов с буквы М по букву Я)
ü Теоретические вопросы:
1. Логистический сервис: понятие, принципы и задачи.
2. Способы уменьшения транспортных расходов.
ü Практическое задание:
Управление запасами в логистике
Оптимальный размер партии поставляемых товаров и, соответственно, оптимальная частота завоза зависят от многих факторов, таких как потребность (спрос), неравномерность расхода, отдаленность поставщиков, ограничения по ресурсам, способы и стоимость транспортировки и ряда других.
Для того чтобы принимать правильные решения по размеру заказываемых партий товаров, необходимо уметь оценивать и сопоставлять возможные варианты поставки.
В качестве критерия оптимальности размера выбирают минимум суммы общих затрат, связанных с размещением заказа и содержанием запаса. При этом учитывают потери, которые возникнут в случае отсутствия запасов, а также возможные ограничения по ресурсам.
Рассмотрим следующую ситуацию:
• потребность за период (спрос) является величиной известной и постоянной;
• удельные транспортно-заготовительные расходы, связанные с доставкой одного заказа, известны и постоянны;
• удельные расходы по хранению запаса (стоимость хранения единицы запаса в единицу времени) известны и постоянны;
• закупочная стоимость товара не зависит от размера закупаемой партии.
Если в этих условиях менять размер заказа, то будет меняться и число заказов за период, а, следовательно, и суммарные за период транспортно-заготовительные расходы, и расходы по хранению (не удельные, а суммарные за период!). Однако характер зависимости каждой из этих статей расходов от объема заказа разный. Суммарные за период транспортно-заготовительные расходы при увеличении размера заказа, очевидно, уменьшаются, так как закупки и перевозки осуществляются более крупными партиями, и, следовательно, реже. Расходы по хранению растут прямо пропорционально размеру заказа.
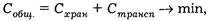 |
Для определения оптимального размера заказа необходимо минимизировать функцию, представляющую сумму транспортно-заготовительных расходов и расходов на хранение от размера заказа, т. е. определить условия, при которых
где Собщ— общие затраты на транспортировку и хранение запаса;
Схран— затраты на хранение запаса за период;
С трансп— транспортно-заготовительные расходы за период.
Предположим, что за определенный период времени Т величина оборота составляет Q. Размер одной заказываемой и доставляемой партии — S. Допустим, что новая партия завозится после того, как предыдущая полностью закончилась. Тогда средняя величина запаса составит — S/2.
Введем размер тарифа Мза хранение единицы запаса в единицу времени. Этот тариф измеряется долей, которую составляют издержки по хранению за период Т в стоимости среднего запаса за этот же период. Например, если М = 0,3, то это означает, что издержки по хранению запаса за период составили 30% от стоимости среднего запаса за этот же период. Можно сказать также, что издержки по хранению единицы товара в течение периода составили 30% от ее стоимости.
 |
Теперь можно рассчитать, во что обойдется хранение товаров за период Т:
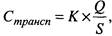 |
Размер транспортно-заготовительных расходов за период Т определится умножением количества заказов за этот период на величину расходов, связанных с размещением и доставкой одного заказа.
где К— транспортно-заготовительные расходы, связанные Я с размещением и доставкой одного заказа;
Q/S — количество заказов за период времени Т.
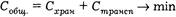 |
Выполнив ряд преобразований, найдем оптимальный—Я размер единовременно доставляемой партии (Sопт),при котором величина суммарных затрат на хранение и заказа будет минимальной.
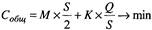 |
или
Функция суммарных затрат имеет минимум в точке, в которой ее первая производная по S равна нулю, а вторая производная больше нуля. Найдем первую производную:
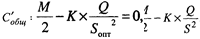 |
Найдем значение Sonт, обращающее производную целевой функции в ноль:
 |
откуда
Проверка показывает, что вторая производная больше нуля, следовательно, полученное значение S обеспечивает минимум совокупных расходов на доставку и хранение.
Полученная формула, позволяющая рассчитать оптимальный размер заказа, в теории управления запасами известна как формула Уилсона.
Рассмотрим пример расчета оптимального размера заказываемой партии. В качестве исходных данных примем следующие величины:
- стоимость единицы товара — 240 долл. (0,24 тыс. долл.);
- годовой оборот склада по данной товарной позиции: Q=7200 ед./год или Q=1728 тыс. долл./год;
- доля затрат на хранение товара составляет 30% от его стоимости, т. е. М = 0,3;
- транспортно-заготовительные расходы, связанные с размещением и доставкой одного заказа:
К = 0,2 тыс. долл.
Тогда оптимальный размер завозимой партии составит:
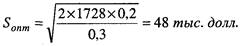 |
Расчет примет несколько иную форму, если объем оборота выразить в натуральных единицах:
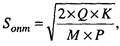 |
где Q — объем оборота, выраженный в натуральных единицах (в нашем случае Q = 7200 ед./год);
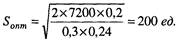 |
Р — стоимость единицы товара (в нашем случае Р = 0,24 тыс. долл.).
Очевидно, что товар в течение года целесообразно завозить 36 раз:
1728 тыс. долл. : 48 тыс. долл. = 36 раз.
В случае заказа партиями оптимального размера транспортно-заготовительные расходы и расходы по хранению составят:
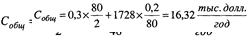 |
Игнорирование полученных результатов приведет кзавышенным расходам. Например, при завозе партиями в 80 тыс. долл. (т. е. S= 80) общие расходы составят:
Задание: Определить превышение фактических расходов, связанных с созданием и поддержанием запасов, над минимальными расходами в случае заказа партии оптимального размера.
Исходные данные для решения задания приведены в таблице 1.
Таблица 1. Исходные данные