УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА РЕАКТОРА
Основой для расчета реакторов с учетом теплового режима служит уравнение теплового баланса, составленное обычно на единицу времени. В общем виде это уравнение может быть записано следующим образом:
(9)
Для экзотермической реакции приход и расход тепла
(10)
(11)
где
Qпр – количество тепла, поступающего в единицу времени в тот реакционный объем, для которого составляется баланс;
Qрасх– количествотепла, расходуемого в единицу времени в реакционном объеме.
Qреаг – количество тепла, вносимого исходными реагентами;
Qх.р – количество тепла, выделяющегося при химической реакции; Qнак – количество тепла, накапливающегося в реакторе;
Qпрод – количество тепла, уносимого продуктами;
QT – количество тепла, выводимого в результате теплообмена.
Подставив значения Qпр и Qрасх в уравнение (9), находим
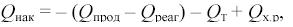(12)
Здесь Qконв – обозначает количество тепла, выносимого конвективным потоком, с учетом которого получим
(13)
Полученное уравнение теплового баланса (13) может принимать различную форму в зависимости от типа реактора и теплового режима процесса.
В общем случае температура и другие параметры процесса изменяются как в объеме реактора, так и во времени, поэтому уравнения теплового баланса составляют в дифференциальной форме (подобно тому, как это было принято при составлении уравнения материального баланса).
Для этой цели используют дифференциальное уравнение конвективного теплообмена
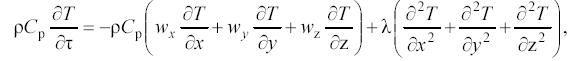(14)
где 
, Сp – плотность и удельная теплоемкость реакционной смеси;
х, y, z – пространственные координаты;
wx, wy, wz – составляющие скорости движения потока в направлении осей;
λ – коэффициент теплопроводности реакционной смеси.
Чтобы использовать это уравнение по отношению к простой необратимой реакции A → R + Q,
его составляют по одному из компонентов реакционной смеси (любому) и
вводят в него дополнительные члены, учитывающие отвод тепла в результате теплообмена и тепло реакции.
Если составить баланс по компоненту А и ввести в уравнение (14) дополнительные члены в соответствии с уравнением (
(13)), то дифференциальное уравнение конвективного теплообмена (уравнение теплового баланса) может быть записано в виде
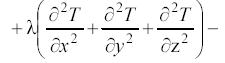
(15)
Левая часть уравнения (15) характеризует скорость накопления тепла в элементарном объеме, для которого составляется тепловой баланс. Этому члену соответствует величина в уравнении (12)
Первая группа членов правой части уравнения (15) определяет скорость конвективного переноса тепла по соответствующим координатам (х, у, z) в элементарном объеме.
Вторая – скорость отвода тепла в результате молекулярной и конвективной теплопроводности реакционной среды.
Первая и вторая группы членов правой части уравнения (15) соответствуют параметру Qконв в уравнении (12):
(16)
Новые, вводимые в уравнение (15) группы членов
характеризуют скорость отвода тепла путем теплообмена (третья группа)
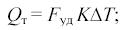(17)
и скорость подвода тепла в результате химической реакции (четвёртая группа)
(18)
где Fуд – удельная поверхность теплообмена;
К – коэффициент теплопередачи;
; (Т, Тхл – температура реакционной смеси и хладоагента);
Н – тепловой эффект химической реакции.
Общее решение уравнения (15) затруднительно, поэтому в зависимости от характера реакции, теплового режима и режима движения реакционной среды (т.е. от гидродинамической обстановки в реакторе), в уравнение (15) вводят соответствующие упрощения. Это позволяет найти решение соответствующей задачи с достаточной для практических целей точностью.
Политропический режим представляет собой общий случай, т.е. при составлении теплового баланса такого реактора учитываются все виды подвода и отвода тепла.
Из уравнения теплового баланса для политропического реактора легко определить частные случаи:
• для адиабатического реактора – с учетом равенства Qт = 0;
• для изотермического реактора – с учетом равенства QКОНВ = 0.
Рассмотрим для примера реактор идеального смешения непрерывный РИС-Н-П, работающий в политропическом тепловом режиме (П).
Отвод или подвод тепла для РИС-Н-П осуществляется через стенку реактора или с помощью теплообменных элементов, расположенных внутри реактора
