УРАВНЕНИЕ МАТЕРИАЛЬНОГО БАЛАНСА РЕАКТОРА
Основанием для получения уравнения реактора любого типа является материальный баланс, составленный по одному из компонентов реакционной смеси.
Составим такой баланс по исходному реагенту A при проведении простой необратимой реакции A → R.
В общем виде уравнение материального баланса:
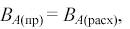(2)
где ВА(пр) – количество реагента А, поступающего в единицу времени в тот реакционный объем, для которого составляется баланс;
ВА(расх) – количество реагента А, расходуемого в единицу времени в реакционном объеме.
Учитывая, что поступивший в реактор реагент А расходуется в трех направлениях, можно записать:
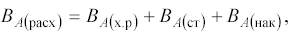(3)
где ВА (х.р)– количество реагента А, вступающее в реакционном объеме в химическую реакцию в единицу времени;
ВА(ст) – сток реагента А, т.е. количество реагента А, выходящее из реакционного объема в единицу времени;
ВА(нак) – накопление реагента А, т.е. количество реагента А, остающееся в реакционном объеме в неизмененном виде в единицу времени.
С учетом уравнения (3) уравнение (2) записывается в виде:
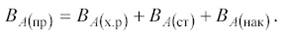(4)
Разность между ВА(пр) и ВА(ст) представляет собой количество реагента А, переносимое конвективным потоком ВА(конв) :
(5)
Принимая это во внимание, уравнение (4) можно записать:
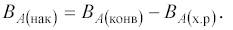(6)
В каждом конкретном случае уравнение материального баланса принимает различную форму.
Баланс может быть составлен
v для единицы объема реакционной массы,
v для бесконечно малого (элементарного) объема,
v а также реактора в целом.
При этом можно рассчитывать материальные потоки,
· проходящие через объем за единицу времени,
· либо относить эти потоки к 1 моль исходного реагента или продукта.
В общем случае, когда концентрация реагента непостоянна в различных точках реактора или непостоянна во времени, материальный баланс составляют в дифференциальной форме для элементарного объема реактора:
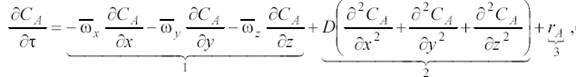(7)
где CA – концентрация реагента А в реакционной смеси;
x, y, z – пространственные координаты;
–составляющие скорости потока;
D – коэффициент молекулярной и конвективной диффузии;
rA – скорость химической реакции.
Левая часть уравнения (7) характеризует общее изменение концентрации исходного вещества во времени в элементарном объеме, для которого составляется материальный баланс. Это – накопление вещества А, которому соответствует величина ВА(нак) в уравнении (6).
Первая группа членов правой части уравнения (7) отражает изменение концентрации реагента А вследствие переноса его реакционной массой в направлении, совпадающем с направлением потока.
Вторая группа членов правой части уравнения (7) отражает изменение концентрации реагента А в элементарном объеме в результате переноса его путем диффузии.
Указанные две группы правой части уравнения характеризуют суммарный перенос вещества в движущейся среде путем конвекции и диффузии. В уравнении (6) им соответствует величина ВА(конв) – такой суммарный перенос вещества называют конвективным массообменом, или конвективной диффузией).
И, наконец, член rA показывает изменение концентрации реагента А в элементарном объеме за счет химической реакции. Ему в уравнении (6) соответствует величина ВА (х.р .
Применительно к типу реактора и режиму его работы дифференциальное уравнение материального баланса (7) может быть преобразовано, что облегчает его решение.
В том случае, когда параметры процесса постоянны во всем объеме реактора и во времени, нет необходимости составлять баланс в дифференциальной форме. Баланс составляют в конечных величинах, взяв разность значений параметров на входе в реактор и на выходе из него.
Все процессы, протекающие в химических реакторах, подразделяют на:
стационарные (установившиеся);
нестационарные (неустановившиеся).
К стационарным относят процессы, при которых в системе или в рассматриваемом элементарном объеме реакционной смеси параметры процесса (например, концентрация реагента А, температура и т.д.) не изменяются во времени, поэтому в реакторах отсутствует накопление вещества (или тепла) и производная от параметра по времени равна нулю.
При нестационарных режимах параметры непостоянны во времени и всегда происходит накопление вещества (тепла).