Минимизация системы ФАЛ
Цель минимизации ФАЛ
МИНИМИЗАЦИЯ функций алгебры ЛОГИКИ
Логическое устройство можно синтезировать непосредственно по алгебраическому выражению, представленному в виде ДНФ или КНФ. Однако полученная схема не будет оптимальной. Поэтому полученные из таблицы истинности ФАЛ необходимо минимизировать.
Целью минимизации ФАЛ является снижение стоимости её технической реализации. Если проанализировать формулу ДНФ (1.2), то можно заметить, что в ней возможны вынесения за скобки общих сомножителей (значений переменных или их инверсий). Такие же преобразования можно провести и в формуле КНФ (1.3), если алгебраически перемножить элементарные логические суммы, а затем привести подобные члены и вынести за скобки общие сомножители. В конечном итоге можно получить выражение, содержащее гораздо меньше переменных. Например, для формулы (1.2) можно провести следующие преобразования:
;
.
Воспользовавшись теоремами №4 
и №1 Х × 1 = Х (см таблицу 1.7), ФАЛ можно ещё более упростить:
. (2.1)
В результате мы получили минимальную дизъюнктивно нормальную функцию МДНФ. Для её технической реализации (без учёта инверторов для получения инверсных значений входных переменных) потребуется шесть ЛЭ: четыре 2И и два 2ИЛИ. В технической реализации по ДНФ из формулы (1.2) требовалось пять элементов: четыре 3И и один 4ИЛИ (см. рис. 1.4).
Попробуем ещё раз преобразовать формулу (1.2):
;
;
.
Воспользовавшись теоремой №11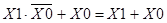 
, получим МДНФ:
. (2.2)
Для технической реализации такой МДНФ потребуется четыре ЛЭ: один 3И, один 2И и два 2ИЛИ.
Мы получили неоднозначные результаты. С одной стороны по ДНФ пять многовходовых (число входов >2) ЛЭ, с другой стороны по МДНФ шесть простых двухвходовых ЛЭ или четыре ЛЭ, из которых один многовходовый. Окончательный выбор варианта технической реализации будет зависеть от типа заданных (или имеющихся в наличии) ЛЭ.
Рассмотренный пример для трёх входных переменных позволил достаточно просто воспользоваться теоремами алгебры логики. Если же входных переменных будет больше, то преобразования становятся не столь очевидными.
2.2. Способ представления ФАЛ с использованием карт Вейча – Карно
Способ представления с использованием карт Вейча – Карно базируется на табличном представлении ФАЛ. Такой способ используется для ручной минимизации, когда количество входных переменных не более пяти.
Карта Вейча – Карно – это прямоугольная таблица, число клеток в которой равно 2n, где n – число переменных. Для каждой клетки ставится в соответствие свой набор входных переменных, а в клетке записывается значение функции (0 или 1) на этом наборе.
 |
Карта для двух входных переменных представлена на рис. 2.1. Она содержит четыре клетки. По краям карты указаны значения входных переменных, которые не изменяются для соответствующих строк и столбцов.
Рис. 2.1. Карта Вейча – Карно для функции двух переменных
 |
Карта для трёх входных переменных представлена на рис. 2.2. Она содержит восемь клеток. Наборы входных переменных крайнего правого и крайнего левого столбцов являются соседними, поэтому пространственно такая карта может быть представлена в виде цилиндра.
Рис. 2.2. Карта Вейча – Карно для функции трёх переменных
Карта для четырёх входных переменных представлена на рис. 2.3. Она содержит шестнадцать клеток. Наборы входных переменных крайнего правого и крайнего левого столбцов, а также нижней и верхней строк являются соседними, поэтому пространственно такая карта может быть представлена в виде тора.
Карта для пяти входных переменных содержит тридцать две клетки. Её можно представить как две карты для четырёх переменных, расположенные одна над другой. Наборы входных переменных крайнего правого и крайнего левого столбцов, а также нижней и верхней строк являются соседними, поэтому пространственно такая карта может быть представлена как два тора, вложенные один в другой. Соседним наборам дополнительно соответствуют клетки, расположенные на разных торах одна под другой. Ввиду сложности работы с такой картой она применяется достаточно редко.
 |
Рис. 2.3. Карта Вейча – Карно для функции четырёх переменных
2.3. Минимизация полностью определённой ФАЛ
При минимизации ФАЛ с помощью карт Вейча – Карно используются либо единичные, либо нулевые значения функции. В обоих случаях получаются равносильные выражения, которые, однако, могут отличаться по числу ЛЭ и выполняемым логическим операциям.
В п.1.5 отмечено, что ФАЛ называется полностью определённой, если заданы все 2n её значений yi. Алгоритм минимизации такой ФАЛ с помощью карт Вейча – Карно следующий:
1) на карте, построенной для ФАЛ, содержащей n-переменных, выделяют прямоугольные области, объединяющие выбранные значения (0 или 1) функции. Каждая область может содержать только 2k клеток, где k – целое число. Выделенные области могут пересекаться, то есть одна или несколько клеток могут принадлежать разным областям.
2) каждой из выделенных областей соответствует самостоятельное логическое произведение входных переменных, значения которых в пределах выделенной области остаются неизменными. Каждое такое произведение содержит (n – k) переменных и называется импликанта.
3) из полученного множества областей выбирают минимальное число максимально больших, включающих в себя все выбранные значения (0 или 1) функции.
4) логически суммируются импликанты, соответствующие выбранным областям. Полученная функция образует МДНФ.
При объединении клеток с единичными значениями ФАЛ получается МДНФ самой функции, а при объединении клеток с нулевыми значениями – МДНФ функции, инверсной заданной.
Применив к полученной инверсной МДНФ теоремы Де-Моргана можно получить минимальную конъюнктивно нормальную функцию (МКНФ).
Рассмотрим пример минимизации ФАЛ, заданной алгебраическим выражением:
. (2.3)
 |
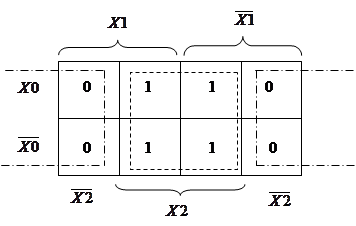Составим карту Вейча – Карно для заданной ФАЛ.
Выделим на карте покрытие, содержащее все единичные значения ФАЛ (выделено пунктиром). Запишем для него значение импликанты, которая будет единственным слагаемым в МДНФ: Y = X2.
Если объединить нулевые значения функции (выделено штрих пунктиром), получим МДНФ, инверсную заданной: 
или Y = X2. В данном простом примере в обоих случаях получилось одно и то же выражение.
Рассмотрим другой пример минимизации ФАЛ, заданной алгебраическим выражением [1]:
. (2.4)
 |
Составим карту Вейча – Карно.
Выделим на карте две области, содержащие все единичные значения ФАЛ (выделено пунктиром). Запишем МДНФ как логическую сумму двух импликант: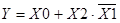 
.
Выделим на карте две области, содержащие все нулевые значения ФАЛ (выделено штрих пунктиром). Запишем МДНФ, инверсную заданной, как логическую сумму двух импликант: 
.
Получились равносильные, но разные выражения. Чтобы доказать равносильность выражений, применим к МДНФ, инверсной заданной, теорему Де-Моргана:
.
Применив к данному выражению теорему №10 (см таблицу 1.7), получим ФАЛ .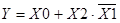
Даже из таких простых примеров видно, что при минимизации по единичным и по нулевым значениям получаются равносильные, но не обязательно одинаковые выражения. Техническая реализация таких логических устройств также будет различной. Используя теоремы алгебры логики выражения можно преобразовать к одинаковому виду, однако преобразования могут быть не очевидны. Поэтому при минимизации желательно рассмотреть оба варианта значений функции и постараться получить наиболее простое выражение, которое будет иметь минимальную стоимость технической реализации.
2.4. Минимизация недоопределённой ФАЛ
ФАЛ называется недоопределённой (частично определённой), если часть её значений yi не задана (см. п. 1.5). При минимизации такой ФАЛ необязательным значениям, которые обычно обозначают *, можно произвольно присваивать единичные или нулевые значения из условия получения на карте Вейча - Карно минимального числа максимально больших областей.
Рассмотрим пример минимизации ФАЛ, заданной таблицей истинности:
| Х3 | Х2 | Х1 | Х0 | Y |
| * | ||||
| * | ||||
| * | ||||
| * | ||||
| * | ||||
| * | ||||
| * | ||||
| * | ||||
| * | ||||
| * | ||||
Составим карту Вейча – Карно.
|
Как видно из карты, ни единичные, ни нулевые значения ФАЛ невозможно объединить друг с другом. Поэтому ДНФ имеет вид
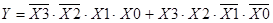, (2.5)
а КНФ
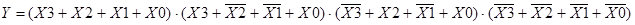. (2.6)
Предположим, что для доопределения ФАЛ принято решение присвоить всем необязательным значениям функции единичные значения. В результате получим следующий вид карты, на которой выделены области единичных значений, и соответствующую МДНФ.
| 
|
Очевидно, что такое решение привело к отрицательному результату. Полученная МДНФ оказалась даже сложнее исходной ДНФ (2.5). Поэтому проведём новое доопределение ФАЛ, добавив единичные значения функции только для получения на карте Вейча - Карно минимального числа максимально больших областей.
| 
|
Поскольку выделить область из восьми клеток не удалось, выбрано решение о выделении двух областей из четырёх клеток каждая. Полученное выражение МДНФ проще исходной ДНФ и требует для своей реализации два инвертора, два элемента 2И и один элемент 2ИЛИ.
Теперь проведём доопределение ФАЛ, добавив нулевые значения функции только для получения на карте Вейча - Карно минимального числа максимально больших областей.
| 
|
Аналогично выделяем две области по четыре клетки в каждой, поскольку выделить область из восьми клеток невозможно. Полученное выражение для МДНФ, инверсной заданной, также содержит логическую сумму двух логических произведений. Для реализации потребуется три инвертора (два для переменных и один для функции), два элемента 2И и один 2ИЛИ.
Для дальнейших преобразований воспользуемся теоремой Де-Моргана:
.
В результате получилось выражение существенно проще, чем исходная КНФ (2.6), для реализации которого потребуется два инвертора, два элемента 2ИЛИ и один элемент 2И. Следует также отметить, что в варианте МКНФ не нужна переменная Х2.
Окончательный выбор варианта технической реализации ФАЛ будет зависеть от типа заданных (или имеющихся в наличии) ЛЭ.
Если логическое устройство имеет m выходов, то его структура описывается системой m ФАЛ. Минимизация структуры такого устройства может быть выполнена с использованием метода карт Вейча – Карно раздельно для каждого выхода. При этом может оказаться, что структура всего устройства получится неоптимальной.
Достижение оптимального результата может быть реализовано выделением в каждом выражении одинаковых импликант, то есть выделением на картах одинаковых областей. Сформировав такую импликанту только один раз, можно использовать её для нескольких из m уравнений, сократив, таким образом, общее число логических элементов в технической реализации логического устройства.
Рассмотрим пример минимизации системы ФАЛ из трёх функций Y1, Y2, Y3 для трёх переменных X2, X1, X0 [1], заданных таблицей истинности.
| X2 | X1 | X0 | Y3 | Y2 | Y1 |
Составим карты Вейча – Карно и проведём минимизацию для получения МДНФ раздельно для каждого выхода.
|  .
| |||
|  .
| |||
|  .
|
Техническая реализация системы ФАЛ, уравнения которой получены раздельно для каждого выхода, потребует три инвертора, семь элементов 2И, два элемента 2ИЛИ и один элемент 3ИЛИ, то есть всего 13 элементов.
Если проанализировать полученные уравнения, можно выделить в них общие члены 
и 
. Сформировав их только один раз, можно упростить техническую реализацию системы ФАЛ. В этом случае потребуется три инвертора, пять элементов 2И, два элемента 2ИЛИ и один элемент 3ИЛИ, то есть всего 11 элементов. Структурная схема такого логического устройства представлена на рис. 2.4.
|
Рис. 2.4. Структурная схема ЛУ для Y1, Y2 и Y3
Нетрудно заметить, что для Y1 не использована область 
, а для Y3 - область . Эти области при раздельной минимизации получаются лишними. Но если стремиться к получению наилучшего результата минимизации системы ФАЛ, можно добавить эти импликанты в соответствующие уравнения, а затем провести дополнительные преобразования по теоремам алгебры логики:
(2.7)
Реализация такой схемы логического устройства потребует три инвертора, четыре элемента 2И и четыре элемента 2ИЛИ, то есть тоже 11 элементов. Однако из схемы исключается элемент 3ИЛИ, что является преимуществом, так как упрощает реализацию. Структурная схема такого логического устройства представлена на рис. 2.5.
|
Рис. 2.5. Структурная схема ЛУ для Y1, Y2 и Y3 по выражению (2.7)
Контрольные вопросы
1. В чём заключается цель минимизации логических устройств?
2. Почему реализация логического устройства по ДНФ или КНФ, полученным непосредственно из таблицы истинности, не будет оптимальной?
3. Почему преобразования по теоремам алгебры логики не всегда могут обеспечить получение минимальной технической реализации логического устройства?
4. Что такое карта Вейча – Карно?
5. Приведите примеры карт Вейча – Карно для двух, трёх и четырёх переменных.
6. Приведите алгоритм минимизации ФАЛ с помощью карт Вейча – Карно.
7. Что такое импликанта?
8. В чём заключается порядок минимизации недоопределённой ФАЛ?
9. Почему замена всех необязательных значений недоопределённой ФАЛ может привести к отрицательному результату минимизации?
10. Почему желательно проводить минимизацию и по единичным и по нулевым значениям ФАЛ?
11. Каковы особенности минимизации системы ФАЛ?
12. Почему минимизация системы ФАЛ раздельно для каждого выхода может привести к неоптимальному результату технической реализации логического устройства в целом?