Принцип двойственности

Структурная схема логического устройства

По полученному алгебраическому выражению ФАЛ можно построить структурную схему логического устройства, используя условные графические обозначения логических элементов (рис. 1.2). Для построения структурной схемы необходимо располагать логические элементы от входа к выходу в порядке записанной ФАЛ. Поскольку для рассматриваемого примера существуют две стандартные формы представления ФАЛ: ДНФ и КНФ, можно построить две структурные схемы, каждая из которых будет соответствовать заданной ФАЛ. Структурная схема логического устройства, построенная по ДНФ, представлена на рис. 1.4.

Рис. 1.4. Структурная схема логического устройства, построенная по ДНФ

Схема содержит три входа по числу входных переменных . Три элемента НЕ (инверторы) позволяют получить инверсные значения входных переменных . Вертикальные линии образуют шины прямых и инверсных значений входных переменных. К этим шинам подключаются входы четырёх элементов 3И, число входов которых равно числу переменных, а количество – количеству слагаемых в алгебраическом выражении ДНФ. Выходы элементов 3И подключены к входам элемента 4ИЛИ, на выходе которого получается значение функции Y = f(X2,X1,X0).

Такую же структурную схему можно построить по КНФ. Структурная схема логического устройства, построенная по КНФ, представлена на рис. 1.5.

Схема так же содержит три входа по числу входных переменных . Три элемента НЕ (инверторы) формируют инверсные значения входных переменных . Вертикальные линии образуют шины прямых и инверсных значений входных переменных. К этим шинам подключаются входы четырёх элементов 3ИЛИ, число входов которых равно числу переменных, а количество – количеству сомножителей в алгебраическом выражении КНФ. Выходы элементов 3ИЛИ подключены к входам

элемента 4И, на выходе которого получается значение функции Y = f(X2,X1,X0).

Рис. 1.5. Структурная схема логического устройства, построенная по КНФ

Принцип двойственности – это свойство взаимного преобразования операций логического сложения и логического умножения. Для доказательства принципа двойственности сравним таблицы истинности операций:

Логическое сложение ИЛИ	Логическое умножение И
Х1 Х0 Х1 + Х0 (Х1 V X0)	Х1 Х0 Х1 × Х0 (Х1 L X0)

Если в логическом сложении значения всех переменных и самой функции заменить их инверсией, то можно получить логическое умножение. Пример такого преобразования представлен в таблице 1.5. Аналогичный пример можно представить и для логического умножения (таблица 1.6).

Таблица 1.5

Преобразование логической операции ИЛИ

Х1	Х0

Таблица 1.6

Преобразование логической операции И

Х1	Х0

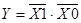
Следовательно, принцип двойственности можно описать следующими выражениями:

(1.4)

Практическим следствием принципа двойственности является тот факт, что при записи логических выражений и построении логических схем можно обойтись только двумя типами операций: только операциями И и НЕ или только операциями ИЛИ и НЕ.

Введём понятие функционально полной системы ЛЭ. Функционально полной системой называется совокупность ЛЭ, позволяющая реализовать логическую схему произвольной сложности. Функционально полной системой является набор операций И, ИЛИ, НЕ. Функционально полными (по принципу двойственности) будут системы с набором операций И, НЕ и ИЛИ, НЕ. Эти операции объединяют в одном логическом элементе. Элемент И-НЕ называется штрих Шеффера, а элемент ИЛИ-НЕ – стрелка Пирса. Условные графические обозначения этих элементов представлены на рис. 1.6.

Рис. 1.6. Условные графические обозначения элементов И-НЕ и ИЛИ-НЕ

Рассмотрим пример реализации основных логических операций на базе элементов 2И-НЕ (рис. 1.7).

Рис. 1.7. Пример реализации основных логических операций на базе элементов 2И-НЕ

На элементах И-НЕ логическая операция И получается с помощью двух элементов. Сначала производится логическое умножение с инверсией, получается . Затем полученный результат ещё раз инвертируется .

Логическая операция ИЛИ на элементах И-НЕ реализуется по принципу двойственности. Сначала входные переменные инвертируются. Инверсные значения на элементе И-НЕ складываются и дополнительно инвертируются (1.4), получается . Инверсия одной входной переменной получается при объединении входов элемента 2И-НЕ. Следует отметить, что число входов логического элемента И-НЕ может быть произвольным.

Аналогичные рассуждения можно применить к логическому элементу 2ИЛИ-НЕ (рис 1.8).

Рис. 1.8. Пример реализации основных логических операций на базе элементов 2ИЛИ-НЕ

Логическая операция И на элементах ИЛИ-НЕ реализуется по принципу двойственности, логическая операция ИЛИ на элементах ИЛИ-НЕ получается с помощью двух элементов, а инверсия одной входной переменной получается при объединении входов элемента 2ИЛИ-НЕ.

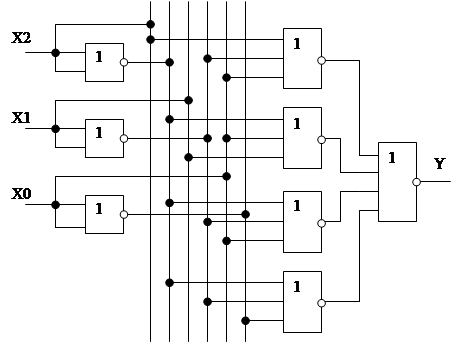В качестве примера реализации логического устройства на элементах ИЛИ-НЕ рассмотрим структурную схему, составленную по КНФ (рис. 1.5). В схеме для реализации операции инвертирования применены элементы 2ИЛИ-НЕ, для получения элементарных логических сумм элементы 3ИЛИ-НЕ, а для логического перемножения по принципу двойственности - элемент 4ИЛИ-НЕ. Схема представлена на рис. 1.9.

Рис. 1.9. Структурная схема логического устройства, построенная на элементах ИЛИ-НЕ