Понятие изокванты. Предельная норма технологического замещения. Изокоста. Равновесие производителя.
Мы могли бы по-иному определить наилучшую комбинацию ресурсов. Фирма, производящая продукт в количестве q, заинтересована в выборе такого варианта производства, который позволил бы получить данный выход продукта при наименьших расходах на приобретение ресурсов. Задача сводится к отысканию на заданной изокванте такой точки, которая располагалась бы на самой низкой изокосте. И в этом случае искомая комбинация изображается точкой касания изокванты и изокосты (рис. 9,б), а для нее должно выполняться соотношение (7).
В отличие от потребителя, доход которого предполагается заданным, для фирмы ни расходы на ресурсы, ни выпуск продукции не являются заданными величинами. И то и другое - результат согласованного выбора с учетом ситуации на рынке продукта. Однако, зная цены ресурсов, мы можем выделить экономически эффективные варианты производственного процесса. Будем называть вариант экономически эффективным, если фирма не может увеличить выпуск продукта без увеличения расходов на ресурсы и не может снизить расходов без сокращения выпуска. На рис. 10. точка Е соответствует эффективному, а точки А и В - неэффективным вариантам: вариант А дороже, чем Е, при том же выходе продукта; варианту В соответствуют те же затраты, что и варианту Е, но выход продукта здесь меньше. Пропорциональность предельных продуктов ценам ресурсов мы можем теперь трактовать как условие экономической эффективности производственного варианта.
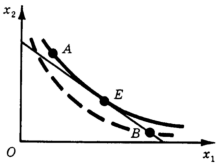
Рис. 10. Экономически эффективный и экономически неэффективный варианты производства
Этот вывод также легко переносится на n -мерный случай. Если комбинация ресурсов (х1, х2, ..., хn) экономически эффективна, то любая пара (xi, xj) peсурсов должна удовлетворять условию вида (7), т. е. равенство
| MPi / MPj = pi/pj |
должно выполняться для любой пары ресурсов. А это возможно, если предельные продукты всех ресурсов пропорциональны ценам:
| MP1 : MP2 : ┼ : MPn = p1 : p2 : ┼: pn. | (8) |
Считая цены ресурсов фиксированными, возьмем на каждой изокванте самую "дешевую" точку (или на каждой изокосте - самую "производительную") и соединим их кривой. Эта кривая объединяет варианты, эффективные при данных ценах ресурсов. Принимая решение об объеме производства, фирма будет оставаться на этой кривой. Ее называют кривой оптимального роста (рис. 11). Приведенные утверждения справедливы в предположении, что фирма может свободно выбирать объемы всех ресурсов. Однако предприятие может в короткий срок резко изменить потребление материалов, может принять на работу требуемое количество работников, но не может столь же быстро изменить, например, производственные площади. В связи с этим различают поведение фирмы в коротком и длительном периодах: в длительном периоде могут изменяться объемы всех ресурсов, в коротком - только некоторых.
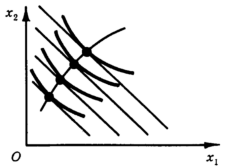
Рис. 11. Кривая роста
Пусть из двух ресурсов, потребляемых предприятием, первый может изменяться в коротком периоде, а второй - только в длительном, в коротком же принимает фиксированное значение х2 = В. Эту ситуацию иллюстрирует рис. 12. В длительном периоде предприятие может выбрать любую комбинацию ресурсов в пределах положительного квадранта плоскости х1х2, а в коротком - лишь на луче ВС.
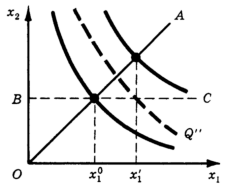
Рис. 12. Изменение масштаба в длительном к коротком периодах
В общем случае все ресурсы можно разделить на изменяющиеся в коротком периоде ("подвижные") и изменяющиеся только в длительном периоде. В коротком периоде могут рационально выбираться лишь объемы "подвижных" ресурсов, так что условие экономической эффективности - пропорция вида (8) - в коротком периоде охватывает только эти виды ресурсов. Вариант, эффективный в коротком периоде, может быть неэффективным в длительном.