Производственная функция Кобба-Дугласа и ее свойства

Функция Кобба-Дугласа получена в результате математического преоб­разования простейшей производственной функции У= F(L, К) в такую мо­дель, которая показывает, какой долей совокупного продукта вознагражда­ется участвующий в его создании фактор производства. Она имеет следую­щий вид:

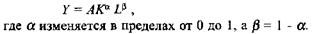
Функция Кобба-Дугласа - модель с двумя переменными факторами производства. Параметр А - коэффициент, отражающий уровень техно­логической производительности и в краткосрочном периоде он не изме­няется. Показатели а и j3- коэффициенты эластичности объема выпус­ка (К) по фактору производства, т. е. по капиталу К и труду L соответ­ственно. При этом, если каждый из факторов оплачивается в соответ­ствии со своим предельным продуктом, то а и /3 показывают доли капи­тала и труда в совокупном доходе. Иными словами, если цена капита­ла равна предельному продукту капитала, а цена труда равна предель­ному продукту труда, то параметры а и /3 определяют пропорцию, в ко­торой труд и капитал получают свое вознаграждение за созданный про­дукт, т. е. долю капитала в доходе aY и долю труда в доходе /3Y. Так как /3= 1 - α, то а + /3= 1, из чего следует, что мы имеем дело с постоянной отдачей от масштаба. Интересно рассмотреть эмпирические значения параметров функции Кобба-Дугласа: А = 1,1; а = 1/4; /J = 3/4.Следовательно, доля капитала в национальном доходе составляет 25%, а доля тру­да - 75%.

В поисках путей наибольшей эффективности производства нас всегда должна интересовать предельная производительность участвующих в нем факторов', с помощью которой определяется оптимальный объем исполь­зуемых ресурсов. Предельный продукт капитала МР_К пропорционален от­ношению доли капитала в доходе к объему использованного капитала: МР_к = аУ/ К. Аналогично определяется и предельная производительность труда: MP_L =/3Y/L.

Рассмотрим свойства производственной функции Кобба-Дугласа.

Первое свойство - постоянство отдачи от масштаба- описывается формулой F(nK,nL) = п А К°Ь^В и означает, что если увеличить использова­ние капитала и труда в n раз, то объем совокупного выпуска, или объем до­хода, возрастет в такое же число раз.

Второе важное свойство функции Кобба-Дугласа связано с изменением предельной производительности факторов.Например, если привлечь в производство дополнительное количество капитала К, а труд L использо­вать в прежнем объеме, то, при прочих равных условиях, предельная про­изводительность труда MP_L увеличится, а предельная производительность возросшего объема капитала МР_к снизится. Если же увеличить количество труда, при прочих равных условиях, то его предельная производительность снизится, а предельная производительность капитала возрастет. Вывод: нарушение пропорции между трудом и капиталом при заданной техноло­гии приводит к отклонению от оптимального объема производства, т. е. к неэффективности производства.

Однако, если мы увеличим параметр Л, например, внедрив более произ­водительную технологию, то получим одновременное повышение МР_к и MP_V что является условием интенсивного экономического роста.

Третье свойство производственной функции Кобба-Дугласа ~ постоян­ство отношения дохода от труда к доходу от капитала(Р/а), т. е. посто­янство соотношения долей капитала и труда в национальном продукте.

Исследования американского сенатора и экономиста Пола Дугласа по­казали, что в Соединенных Штатах за сорок лет (с 1948 по 1989 гг.) соот­ношение р/аколебалось в пределах между 2 и З², в результате чего оплата труда в 2-3 раза превышала вознаграждение капитала.¹ Можно предполо­жить, что постоянные рамки колебания соотношения |3/азаданы техноло­гически. Колебания /5/авнутри этих рамок могут быть объяснены откло­нением в соотношении / и S, так как вряд ли заработная плата, шкала на­логообложения и нормы амортизации почти ежегодно могли претерпевать значительные изменения.

Макроэкономическое равенство /= 5лежит в основе механизма эконо­мического роста еще одной неоклассической модели, которая также бази­руется на производственной функции. Она называется моделью роста Со-лоу, по имени американского экономиста, лауреата Нобелевской премии Роберта Солоу.