Теория предель­ной производительности факторов. Изокоста. Оптимум фирмы

 

Анализ теории предельной производительности факторов требует рас­смотрения таких понятий, как общий, предельный и средний продукт переменного фактора производства. Общий продукт (ТР)- это суммар­ный объем выпуска продукции, полученный в рамках заданной произ­водственной функции, и измеренный в физических единицах. Понятие общего продукта позволяет выявить зависимость между объе­мом выпускаемой продукции и изменениями в количестве одного ресурса при неизменном количестве других. Предположим, что фирма использует 2 ед. капитала. Тогда производ­ственная функция будет представлена данными, содержащимися во второй строке таблицы (см. Табл. Альтернативные способы производства продукции (телевизоры, шт) - выше). Как видно из ее данных, при использовании 2 ед. ка­питала общий объем производства будет зависеть от количества использу­емых единиц труда. Таким образом, общий продукт переменного фактора L может быть описан следующей производственной функцией:

 

Q= F (L) , при К— const

 

Это уравнение выражает отношение между общим выпуском продукции и количеством фактора L, при условии, что количество фактора К постоян­но и равно 2 ед. Графически данная производственная функция будет иметь следующий вид:

 

 

Кривая производственной функции построена на основе данных табл. «Альтернативные способы производства продукции (телевизоры, шт)» и показывает зависимость между объемом выпускаемой продук­ции и затратами одного переменного фактора L при неизменном количестве фактора К (К=2). Очевидно, что, если количество используемого фактора К будет зафиксировано на другом уровне, то производственная функция, описывающая общий объем выпуска фактора L, будет иметь иной вид.

Предельный продукт фактора производства (MP_L), исчисленный в физических единицах, показывает изменение в объеме выпуска про­дукции, вызванное использованием дополнительной единицы данного фактора (L) при неизменном количестве всех остальных. Предельный продукт фактора может быть исчислен следующим образом:

 

МР_L = ∆Q / ∆L

 

где MP_L - предельный продукт фактора L, ∆Q - изменение общего объе­ма выпуска продукции, ∆L - изменение количества фактора L.

Средний продукт фактора (АР_L) определяется путем деления объе­ма выпускаемой продукции на количество используемого переменного фактора L:

 

AP_L = Q / L

 

Средний продукт труда показывает, какое количество произведенной продукции приходится на одну единицу труда. Очень часто средний продукт называют показателем производительности труда.

Рассмотрим двухфакторную производственную функцию на примере обувной фабрики. Предположим, что количество используемых в производстве станков является неизменным и равно 7 ед., т. е. капитал - величина постоянная. Затраты переменного фактора труда измеряются количеством рабочих. Данные об общем, предельном и среднем продукте переменного фактора в рамках нашей производственной функции представлены в таб­лице ниже.

 

Табл. Общий, предельный и средний продукт труда при производстве обуви

 

Число занятых в день рабочих	TPL в день (десятки пар)	MPL (MPL= ∆Q / ∆L)	APL (APL=Q / L)
	0,5	0,5	0,5
	1,2	0,7	0,6
	2,1	0,9	0,7
	3,5	1,4	0,87
	4,5	1,0	0,9
	4,8	0,3	0,8
	4,8		0,68
	4,6	-0,2	0,57
	4,3	-0,3	0,47
	3,6	-0,7	0,36

 

 

На основе данных таблицы построим кривые общего, предельного и среднего продукта переменного фактора и проанализируем их.

Как видно из рисунка а (см. ниже), кривая общего продукта (ТР) проходит три стадии, каждой из которых соответствуют отрезки кривой, ограниченные точками А, В, С, представляющими особый интерес. Следует заметить, что каждая из этих трех точек имеет свою проекцию на кривых предельного и среднего продукта - точки А', В', С (см. рис. б).

Точка А на отрезке ОА представляет собой точку изгиба, где кривая об­щего продукта изменяет свою выпуклость. Это связано с тем, что рост об­щего продукта ускоряется до этой точки (в нашем примере ей соответству­ет общий продукт, равный 3,5 десятков пар обуви), так как предельный продукт переменного фактора L на отрезке ОА устойчиво и быстро растет. Это означает, что каждая дополнительная единица фактора L увеличивает общий объем производства на большую величину по сравнению с преды­дущей. Именно точка А на кривой общего продукта соответствует макси­мальному значению предельного продукта (в нашем примере он равен 1,4 десятка пар обуви).

На отрезке АС рост общего продукта замедляется, так как предельный продукт фактора L начинает устойчиво снижаться, хотя и имеет положи­тельное значение. Это означает, что каждая дополнительная единица фак­тора L увеличивает общий объем производства на меньшую величину по сравнению с предыдущей. Поэтому на отрезке АС кривая общего продукта изменяет свою выпуклость по отношению к отрезку ОА. Точка В на кривой (TP_L) показывает ту величину общего продукта, при которой предель­ный и средний продукт равны. В точке С общий продукт достигает своего максимального значения (в нашем примере 4,8 десятка пар обуви), а пре­дельный продукт равен 0.

После точки С кривая общего продукта начинает снижаться, так как предельный продукт принимает отрицательные значения. Это означает, что дальнейшее увеличение количества переменного фактора приведет к сокра­щению величины общего продукта.

 

 

Существует определенная зависимость между предельным и средним продуктом переменного фактора, что хорошо видно на графике (см. рис. б ). Предельный продукт достигает своего максимального значения раньше, чем средний продукт. Когда величина предельного продукта пре­вышает величину среднего продукта, тогда кривая АР_L возрастает и наобо­рот, когда величина предельного продукта меньше величины среднего про­дукта, кривая АР_L убывает. Из этого следует, что кривая предельного про­дукта (MP_L) пересекает кривую среднего продукта (АР_L) в точке максиму­мапоследнего.

Рассмотренные выше кривые общего и предельного продукта отражают тенденцию, известную как закон убывающей предельной производи­тельности (доходности) факторов производства. Этот закон гласит, что, по мере увеличения количества переменного фактора при неизменном ко­личестве всех остальных будет достигнут такой рубеж, после которого пре­дельный продукт переменного фактора начнет уменьшаться. Данный закон не имеет четкой системы доказательств, он основан на здравом смысле и эмпирических наблюдениях. Закон убывающей предельной производительности факторов можно проиллюстрировать на примере нашей обувной фабрики (см. Табл. «Общий, предельный и средний продукт труда при производстве обуви»). Если фирма наймет одного рабочего, то при существующей техно­логии он не сможет обслуживать одновременно все семь станков. Очевид­но, что при такой комбинации труда и капитала выпуск продукции будет весьма невелик. Если фирма привлечет несколько дополнительных рабо­чих, так, чтобы они смогли использовать все семь станков, то выпуск обу­ви резко увеличится. Это означает, что предельный продукт каждого допол­нительного рабочего возрастает. Если фирма будет продолжать увеличивать количество рабочих, то станочный парк окажется слишком маленьким для них, и предельный продукт каждого из этих рабочих начнет постепенно снижаться до тех пор, пока не достигнет нуля. Соответственно, темп при­роста общего продукта замедлится. И, наконец, мы столкнемся с ситуаци­ей, когда предельный продукт еще одного дополнительно нанятого рабоче­го примет отрицательное значение, так как для равномерной загрузки ра­бочих предприниматель вынужден будет чередовать их работу у станков. Это неизбежно приведет к потере времени функционирования станков и соответственно к снижению объема выпускаемой продукции. В нашем при­мере это восьмой нанятый рабочий.

Таким образом, теория предельной производительности факторов име­ет исключительно важное значение для определения оптимального сочета­ния факторов при выпуске продукции.

Уже известная нам предельная норма технологического замещения (MRTS) непосредственно связа­на с предельными продуктами факторов производства. Сокращая количество одного из факторов, например капитала (∆К), фирма тем самым уменьшает объем выпуска продукции на определенную величину. Эта ве­личина равна произведению предельного продукта капитала (МР_К) и изме­нения в его количестве (∆K):

∆Q = MP_K ∙ (-∆K)

где ∆Q - изменение в объеме выпуска продукции; МР_К- предельный продукт капитала; ∆K - изменение количества применяемого капитала.

Для того, чтобы остаться на той же изокванте, сокращение объема про­изводства должно быть компенсировано увеличением количества применя­емого труда (∆L), т. е.

∆Q = MP_L ∙ ∆L

Где MP_L - предельный продукт труда; ∆L -изменение количества применяемого труда.

Это означает, что абсолютное значение ∆Q в уравнениях должно быть одинаковым. Следовательно, можно записать:

 

MP_K ∙ (-∆K)= MP_L ∙ ∆L

 

Отсюда следует, что MRTS_KL = -∆K / ∆L = MP_L / MP_K = наклону изокванты

 

 

Фирма, осуществляющая свою деятельность с использованием двух пе­ременных частично взаимозаменяемых факторов, сталкивается с пробле­мой оптимального выбора комбинации ресурсовпри каждом заданном объеме выпуска продукции. Очевидно, что фирма, максимизирующая прибыль, будет стремиться выбрать такое сочетание ресурсов, которое окажется самым дешевым. Таким образом, задача сводится к тому, что­бы минимизировать издержки фирмы для каждого заданного объема про­изводства. Для решения поставленной задачи необходимо ввести понятие изокосты.

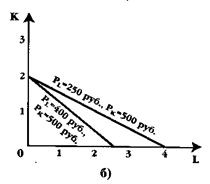
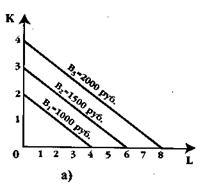
Изокостаявляется одновременно и линией равных издержек, и линией бюджетного ограничения фирмы. Изокоста строится следующим образом. Допустим, что бюджет фирмы для закупки факторов, например, капитала и труда, составляет 1000 руб. Цена 1 ед. капитала равна 500 руб., а 1 ед. труда - 250 руб. Если в рамках заданного бюджета фирма затратит деньги на покупку только одного из двух факторов, то она сможет купить либо 2 ед. капитала, либо 4 ед. труда. Отметим на графике точки, соответствующие этой комбинации факторов (см. рис. а). Соединив эти точки, мы получим изокосту.

 

 

Любая точка на изокосте показывает такое сочетание двух факторов, при котором совокупные расходы на их приобретение будут равны. Изокосты, изображенные на рис. б, описываются следующим уравнением:

 

B = P_K · K + P_L ∙ L

 

где В - бюджет фирмы, предназначенный для закупки факторов; Рк— цена единицы капитала; К - количество капитала; P_L - цена единицы труда; L - количество труда.

Наклон изокосты равен отношению цен используемых факторов ум­ноженному на (-1), так как изокоста имеет отрицательный наклон. Ина­че говоря, если фирма увеличивает количество одного фактора, то она должна соответственно сократить использование другого, чтобы сохра­нить неизменными совокупные расходы на приобретение факторов, т. е.

P_L ∙ ∆L = - (P_K · ∆K)

Отсюда следует, что

-∆K / ∆L = P_L / P_K

 

Любое изменение цены на один из двух используемых ресурсов ведет к изменению наклона изокосты. В случае, когда изменяется заданная величина бюджета фирмы, предназначенного на покупку ресурсов, изокосты сдвигаются влево или вправо в зависимости от того, уменьшилась или возросла сумма бюджета (см. рис. а ).

Для ответа на поставленный выше вопрос, какое сочетание факторов для каждого заданного объема выпуска является самым дешевым, необхо­димо совместить карту изоквант с изокостами. Точки касания изокост с изоквантами покажут оптимальное, с точки зрения затрат, сочетание фак­торов для каждого заданного объема выпуска продукции (см. рис. ниже).

 

Комбинация факторов в точке А обеспечит наименьшие издержки при объеме выпуска продукции, равном Q₁; в точке В - объеме, равном Q₂; в точке С - объеме, равном Q₃.Все другие возможные комбинации факто­ров, принадлежащие изоквантам с объемом производства соответственно Q₁, Q_2, Q₃ лежат на более высоких линиях бюджетного ограничения. Соединив точки А, В, С мы получим кривую, показывающую оптималь­ные комбинации ресурсов при существующих ценах на них для каждого заданного объема выпуска продук­ции. Принимая решение об объемах производства, фирма будет двигаться вдоль данной кривой, которую принято называть траекторией роста.

Тот факт, что минимизация издержек достигает­ся в точке касания изокосты и изокван­ты, позволяет сделать важный эконо­мический вывод. Как известно, наклон изокосты равен отношению цен на фак­торы (P_L / P_K), а наклон изокванты ра­вен MRTS_KL, которая вычисляется по формуле выше. В точке касания наклон изокосты равен наклону изокванты. Следовательно, равновесие достигает­ся тогда, когда отношение цен на факторы равно отношению их предельных продуктов, т. е.

P_L / P_K = MP_L / MP_K

Соответственно, отношения предельных продуктов факторов к ценам последних должны быть равны между собой:

MP_L / P_L = MP_K / P_K