I.Статические методы

ОЦЕНКА АЛЬТЕРНАТИВНЫХ ИНВЕСТИЦИЙ

При оценке альтернативных инвестиций необходимо сделать вы­бор одного (иногда нескольких) проектов, основываясь на каких-то показателях, например, ЧДД, ИД, ВНД.

При оценке альтернативных инвестиционных проектов можно столкнуться с ситуацией, когда разные показатели приемлемости ин­вестиций приводят к противоречивым выводам (очень редко ветречается ситуация, когда инвестиция оказывается выгодной абсолют­но по всем критериям оценки). Поэтому мы рассмотрим возможно­сти для принятия инвестиционных решений по выбору лучшего ин­вестиционного проекта при противоречивости аналитической информации.

Рассмотрим способы оценки альтернативных инвестиций.

Способы оценки альтернативных инвестиций статическими ме­тодами базируются на следующей информации: общий объем инвестиций по проекту — И;

годовые текущие издержки на производство продукции — 3;

годовая выручка от реализации продукции — В;

годовая прибыль по инвестиционному проекту — ПР = В - 3.

Очень редко, но могут быть случаи, когда выбор лучшего инве­стиционного проекта очевиден:

 

I	II	III	IV	V
И1 = И2	И1<И2	И1 <И2	И1<И2	ит.д
31<3	31 = 32	31 <32	ПР1>ПР2
1 вариант	1 вариант	1 вариант	1вариант
лучше	лучше	лучше	лучше

Рассмотрим статические методы выбора инвестиционных проек­тов, когда выбор неочевиден.

1. Метод сравнения издержек (расчетное сопоставление затрат). Метод базируется на данных об издержках,которые порождает инве­стиционный проект для каждого периода (а не на денежных пото­ках). Критерий эффективности инвестиций: сравнение затрат меж­ду альтернативными инвестициями (затраты определяются на единицу готовой продукции — объем производства), причем учитываются толь­ко затраты, зависящие от данной инвестиции.

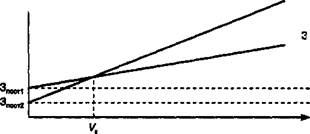
Пример 1. Допустим, нам надо выбрать станок из двух предло­женных. При этом затраты З_{пост 1} > З_{пост 2}, а З_{пер 1} < З_{пер 2}. Решение пред­ставлено в графической форме (рис. 1).

При V < V_K — 2 вариант лучше (суммарные издержки ниже);

при V> V_K— 1 вариант лучше (суммарные издержки ниже).

Общая оценка метода приведена в табл. 1.

Затраты

З_пер2

Объем производства V

 

Рис .1 – Метод сравнения издержек

 

Таблица 1- Достоинства м недостатки метода сравнения издержек

Достоинства

Недостатки

1. Относительная простота 2. Не требуются расчеты прибыли

1. При расчете затрат на единицу продукции не учитывается разная загрузка производственных мощностей 2. Достоверен (реалистичен) только в краткосрочном периоде, так как издержки постоянны только в небольшом промежутке времени (при изменении издержек изменится и VK) 3. Не учитывается остаточная стоимость заменяемого обору­дования (выручка от ликвидации) 4. Не учитываются доходы от инвестиций (инвестиционные доходы)

 

Область применения метода:

—если доходы всех альтернативных инвестиций равны, а затраты во времени постоянны;

—когда сложно рассчитать выручку от реализации продукции, а значит, и прибыль (например, для одного станка);

—когда выгоды по проекту трудно оценить в денежном выраже­нии (социальные проекты);

—когда выгоды от инвестиционного проекта не будет, но инве­стиции являются вынужденными (выбор вида освещения, противопо­жарных мероприятий, ООС и т.п.).

2.Метод расчетного сопоставления прибыли. Сущность: срав­нение годовой прибыли альтернативных инвестиций (ПР = В - 3). Са­мой выгодной является инвестиция, зарабатывающая самую высокую прибыль.

Общая оценка метода представлена в табл. 2.

Таблица 2- Достоинства м недостатки метода

Достоинства	Недостатки
1. Относительная простота 2. Учет не только затрат, но и доходов	1. Должна быть одинаковая производственная мощность по проектам (объем производства) 2. Не учитываются доходы от реинвестирования прибыли 3. Абсолютный показатель, т.е. не учитывается размер инвестиций 4. Необходим расчет доходов по проекту

 

При разном размере инвестиций можно рассчитать доходность инвестиций по проектам:

R_и = ПР/И → max

 

3. Метод расчета сравнительной эффективности инвестиций. Используется в следующей ситуации: И₁> И₂; 3₁ < 3₂ (С_с1 < С_с2).

Сущность метода:определение эффективности дополнительных инвестиций по одному из вариантов. При этом можно использовать два показателя.

а. Срок окупаемости дополнительных инвестиций. Срок окупа­емости дополнительных инвестиций определяет период времени, за который дополнительные инвестиции по одному из проектов окупят­ся снижением себестоимости продукции по этому проекту:

Т^с_ок = И₁ – И₂ / С_с2 - С_с1 = ∆И / ∆С_с < Т^н_ок → min

где И_i — инвестиции по вариантам;

С_сi — себестоимость готовой продукции по вариантам;

∆И — дополнительные инвестиции по одному из вариантов;

∆Сс — снижение себестоимости продукции по варианту с большими ин­вестициями;

Т^н_ок — нормативный срок окупаемости инвестиций.

 

б. Коэффициент сравнительной эффективности инвестиций:

 

Ес= С_с2 - С_с1 / И₁ – И₂ = ∆С_с /∆И →max

По экономическому содержанию ∆С_С — дополнительная прибыль по одному из вариантов, возникающая вследствие более низкой себе­стоимости. Коэффициент сравнительной эффективности инвестиций определяет доходность дополнительных инвестиций за счет снижения себестоимости.

Общая оценка метода дана в табл. 3.

Таблица 3 Достоинства и недостатки метода

Достоинства	Недостатки
1. Не требуется рассчитывать выручку от реализации и прибыль	1. Усложнение расчетов при количестве вариантов больше двух 2.Выручка по всем вариантам д.б.одинаковой

II. Методы, основанные на дисконтированных оценках с теоре­тической точки зрения, являются более обоснованными, поскольку учитывают фактор времени. Вместе с тем они относительно более тру­доемки в вычислительном плане. Из всех рассмотренных критериев наиболее приемлемыми для принятия решений инвестиционного характера являются методы расчета NPV, ИД и ВНД. Вариант, у которого эти показатели максимальны, будет лучшим.

Однако, несмотря на отмеченную взаимосвязь между этими пока­зателями, при оценке альтернативных инвестиций проблема выбора критерия остается, так как чаще всего результаты расчетов про­тиворечат друг другу. Рассмотрим это на примере.

Пример1. Выберем лучший вариант ИП из 3 альтернативных инвестиций при норма дисконта 10%.

Проекты	Начальный период (инвестиции)	Доходы 1 год	2 год	3 год	ЧДД	ИД	ВНД
А						1,455	30,8%
В						1,438	32%
С						1.445	35,4%

 

Выводы по расчетам.

1. Максимальный NPV = 105 д.е. имеет проект В, т.е. реализа­ция этого проекта дает наибольший прирост капитала фирмы.

2. Максимальный индекс доходности ИД = 1,455 д.е./д.е. у про­екта А, т.е. текущая стоимость денежного потока на 45,5% превыша­ет величину стартового капитала.

3. Максимальную внутреннюю норму доходности ВНД = 35,4% имеет проект 3.

Следовательно, каждый проект имеет максимальное значение одного из критериев.

Таким образом, при анализе альтернативных проектов критерии NPV, ИД и ВНД могут противоречить друг другу и сложно опреде­лить лучший проект. Причины возникновения противоречия между критериями:

масштаб проекта, т.е. значительное отличие элементов денеж­ных потоков одного проекта от элементов другого проекта;

интенсивность потока денежных средств, т.е. временное рас­пределение максимальных денежных потоков на первые или преиму­щественно на последние годы жизни проекта.

В случае противоречивости показателей за основу следует брать NPV, так как он характеризует возможный прирост цены фирмы, обладает свойством аддитивности,что позволяет складывать NPV по различным проектам. Однако у показателя NPV есть существенный недостаток: его зависимость от нормы дисконта Е, т.е. при разных значениях нормы дисконта можно получить совершенно противопо­ложные результаты.

Для более достоверного анализа инвестиционных проектов реко­мендуется использовать график зависимости NPV от нормы дисконта NPV =f(E), который:

- представляет нелинейную зависимость;

- пересекает ось У в точке NPV =f(E = 0), т.е. NPV₀ = SД - SИ (недисконтированные);

- пересекает ось X в точке, соответствующей ВНД проекта.

Продолжим решение примера 1. Из дальнейшего рассмотрения исключим проект А, поскольку его NPV и ВНД самые низкие, а ИД чуть выше, чем у проектов 2 и 3.

Показатели проектов В и С противоречивы, поэтому проведем анализ с помощью графиков NPV = f(Е). Для их построения прове­дем дополнительные расчеты:

 

E, %		NPVВ		NPVС
		-240 =		380-220=160
32,0				...
35,4		----

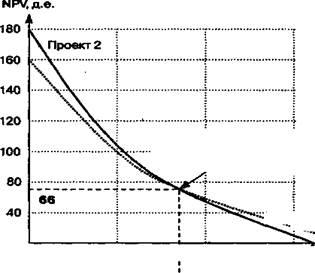
Из рисунка 3 видно, что выбор проекта для реализации зави­сит от принятой ставки Е. При Е = 10% лучшим является проект В, однако если бы норма дисконта Е была равна 20%, то лучшим стал бы проект С. Точка Фишера при Е=17%, при ЧДД = 66 д.е.

Пересечение (точка) Фишера

 

 

10 17 20 30 Е (%)

От 0 до 17% проект В (2) от 17% и дальше – проект С(3)

Рис.3 – Нахождение точки Фишера

Кривые на рис. 3 имеют точку пересечения, которая называется пересечением (или точкой) Фишера (по имени известного экономи­ста Ирвинга Фишера, проанализировавшего этот аспект инвестици­онных расчетов). Характеристики точки Фишера:

1) показывает значение нормы дисконта Е, при которой альтерна­тивные проекты имеют одинаковое значение NPV;

2) пограничная точка, разделяющая ситуации, «улавливаемые» критерием NPV и «не улавливаемые» критерием ВНД:

—если Е > точки Фишера, то NPV и ВНД не противоречат друг другу и оба показывают лучший проект;

—если Е < точки Фишера, то NP V и ВНД противоречат друг дру­гу и лучший проект определяется по максимальному значению NPV.

Причем критерий NPV позволяет выявить лучший вариант в лю­бой ситуации.

Значение нормы дисконта Е в точке Фишера численно равно ВНД приростного потока, т.е. потока, составленного из разностей соответ­ствующих элементов исходных потоков. Для нахождения точки Фишера необходимо:

—составить гипотетический проект (приростный поток);

—найти ВНД этого потока.

Пример 2.Вернемся к предыдущим примерам и определим точку Фишера для проектов В и С.

Составим гипотетический (приростный) поток (рис. 4).

Е = 15% ЧДД приростный = 1,7 д.е.

Проекты	Начальный период (инвестиции)	Доходы 1 год	2 год	3 год
В
С
Приростный поток (В-С)	-20	-40

 

Если Е=17% ЧДД = 0 д.е. , тогда ВНД приростный = 17%

ЧДД проекта В при Е=17% = 64 д.е.

ЧДД проекта С при Е=17% = 64 д.е.