Исходные данные

 

Исходными данными при решении систем линейных алгебраических уравнений прямыми (точными) методами являются:

- размерность системы уравнений n;

- матрица действительных коэффициентов А;

- столбец свободных членов В.

 

Исходными данными при решении систем линейных алгебраических уравнений итерационными методами являются:

- размерность системы уравнений n;

- матрица действительных коэффициентов А;

- столбец свободных членов В;

- заданная точность .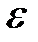

Результатомявляется столбец неизвестных X.

Для ввода матриц и вывода результатов при выполнении задания с использованием C++ Builder наиболее удобно использовать визуальный элемент StringGrid (закладка Additional). Для обеспечения возможности ввода данных с клавиатуры в матрицы А и В необходимо в соответствующих объектах StringGrid установить опцию (Options) goEditing в true. При вводе данных необходимо осуществлять преобразование типа данных - из строкового (тип AnsiString), в котором отображаются вводимые данные в соответствующих визуальных компонентах (StringGrid или Edit), в тип, который будет использоваться при расчетах. Для этого следует использовать стандартные функции класса AnsiString: StrToFloat или ToDouble и StrToInt или ToInt. Для отображения результатов необходимо провести обратные преобразования: FloatToStr и IntToStr.

Вычисления проводить по приведенному выше алгоритму в функции, в которую передаются исходные данные для решения и которая возвращает указатель на массив неизвестных:

double* Gauss (int n, double **a, double *b){...} - пример заголовка функции для точных методов,

double* Zeidel (int n, double **a, double *b, double epsilon){...} - пример заголовка функции для итерационных методов.

Итерационный процесс необходимо реализовать с использованием операторов do {последовательность действий} while (условие),

то есть проводить вычисления до тех пор, пока выполняется условие ( ).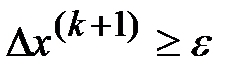

 

Контрольные вопросы

 

1. Какие методы решения систем линейных алгебраических уравнений являются прямыми? Чем они характеризуются?

2. Каково условие существования и единственности решения системы уравнений?

3. Какие методы называются итерационными? В чем их отличие от прямых?

4. Какой метод обеспечивает более быструю сходимость – метод простых итераций или Зейделя?

5. В чем состоит отличие метода Зейделя от метода простых итераций?

6. Для каких порядков систем применяются прямые и итерационные методы?

7. Для чего применяется модифицированный метод Гаусса – метод Гаусса с выбором наибольшего элемента по столбцам?