Методика работы

Лабораторная работа ЭМК-7 К. Изучение законов постоянного тока

Цель работы: овладение методикой исследования цепей постоянного тока.

Задачи:

- изучение обобщенного закона Ома;

- изучение зависимости полезной мощности в цепи постоянного тока от сопротивления нагрузки.

Задание 1. Изучение обобщенного закона Ома.

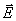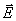В замкнутой электрической цепи, наряду с участками, на которых положительные носители заряда движутся в направлении электрического поля (в сторону убывания потенциала ), должны быть участки, на которых положительные заряды движутся в направлении, противоположном , т.е. в направлении возрастания потенциала. Такое перемещение возможно лишь с помощью сил неэлектростатического происхождения, называемых сторонними силами. Работа сторонних сил по перемещению единичного положительного заряда называется электродвижущей силой (ЭДС). Участок цепи, на котором действуют сторонние силы, называется неоднородным участком.

Работа электростатических (кулоновских) и сторонних сил на участке 1-2 по перемещению заряда равна [1]

. (3.1)

Величина, численно равная работе электростатических и сторонних сил по перемещению единичного положительного заряда, называется падением напряжения или просто напряжением на данном участке (1-2) цепи.

В соответствии с (3.1)

. (3.2)

Из (3.2) следует, что напряжение совпадает с разностью потенциалов лишь на однородном участке, когда нет сторонних сил, т.е. в этом случае .

Падение напряжения U₁₂ на участке цепи можно выразить в виде произведения силы протекающего тока и полного сопротивления данного участка, т.е.

, (3.3)

где – внутреннее сопротивление источника тока.

Приравнивая правые части (3.2) и (3.3) и решая полученное уравнение относительно силы тока, получим выражение закона Ома для неоднородного участка цепи (или обобщенного закона Ома)

. (3.4)

Задание 2. Изучение зависимости полезной мощности в цепи постоянного тока от сопротивления нагрузки.

Полная мощность , выделяемая источником тока в замкнутой цепи, равна

, (3.5)

где - сила тока;

- ЭДС источника.

Полезная мощность , выделяемая на внешней нагрузке , равна произведению напряжения на нагрузке и силы тока , т.е.

. (3.6)

Отношение полезной мощности к полной называется коэффициентом полезного действия источника тока

. (3.7)

Используя закон Ома для полной цепи

где - внутреннее сопротивление источника тока, и закон Ома для участка цепи , полезную мощность можно выразить через ЭДС источника, его внутреннее сопротивление и сопротивление нагрузки

. (3.8)

Это выражение показывает, что при (короткое замыкание) и при (разомкнутая цепь) полезная мощность стремится к нулю. Значит, кривая зависимости полезной мощности от внешней нагрузки имеет максимум. Исследуя выражение (3.3) на экстремум, т.е. приравнивая производную от по нулю , найдем, что максимальное значение полезной мощности достигается при (внешнее сопротивление равно внутреннему). Таким образом, увеличивая сопротивление от нуля и вычисляя каждый раз по (3.2) полезную мощность, можно на опыте убедиться, что она в начале возрастает от нуля, достигает максимального значения, затем вновь стремится к нулю.

Сопротивление , при котором достигается максимум , и будет равно внутреннему сопротивлению источника тока.