ФОРМУЛА ПЛАНКА

Контрольные вопросы к лекции №17

1. Что такое коррозия?

2. По каким признакам классифицируются коррозионные процессы?

3. Что такое межкристаллитная коррозия?

4. Что является причиной электрохимической коррозии?

5. Чем обусловлена химическая коррозия?

6. Какие методы борьбы с коррозией существуют?

Формула Планка дает выражение для равновесной (термодинамическое равновесие)

 

спектральной плотности энергии теплового излучения, т.е. энергии электромагнитного поля, приходящейся на единицу объема и единичный интервал частот около произвольной частоты ν в полости, стенки которой имеют постоянную температуру.

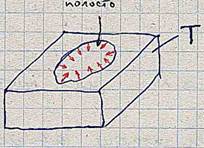
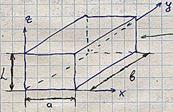
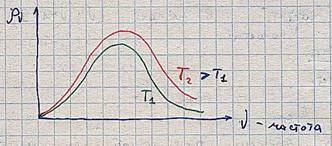Как известно, если температура тела больше абсолютного нуля, то оно излучает в окружающее пространство электромагнитные волны всех частот, произвольных поляризаций и направлений. В замкнутой полости (рис.1) каждый участок внутренней поверхности излучает и на него падает излучение от остальных участков. Падающее излучение частично отражается, частично рассеивается и частично поглощается. Как показывает эксперимент и подсказывает интуиция, через некоторое время после начала эксперимента при поддержании постоянной температуры стенок Т устанавливается динамическое равновесие: количество э/м(электромагнитной) энергии в единичной полосе частот около произвольной частоты ν, поглощаемое любым участком поверхности полости за единицу времени, в среднем остается постоянным во времени (но зависящим от ν и Т) и равным количеству э/м энергии с теми же параметрами, излучаемой этим участком внутрь полости за то же время. При этом в каждой точке полости устанавливается неизменное во времени и пространстве полости среднее значение спектральной плотности теплового (хаотического) излучения ρ_ν(ν,Т)(через ρ_ν(ν,Т) однозначно определяется мощность теплового излучения, падающая на любой участок поверхности полости, а, значит, и величина поглощаемой этим участком э/м мощности). Хаотическим оно называется потому, что считается, что в каждой точке полости полное э/м поле является суперпозицией волн всех направлений, поляризаций, частот и со случайным, статистически независимым, набором амплитуд и фаз. Что, в свою очередь, является следствием независимости и хаотичности излучения различных участков поверхности полости. Зависимость ρ_ν от ν и Т была тщательно измерена экспериментально. Качественно, вид этой зависимости представлен на рис. Второе начало термодинамики требует, чтобы эта зависимость не зависела от формы полости, её размеров и материала стенок (на самом деле это верно только когда линейные размеры полости много больше средней длины волны равновесного излучения).

Теоретики пытались получить эту зависимость аналитически и лишь Планку удалось добиться прекрасного совпадения теории с экспериментом. Это было достигнуто в предположении квантованности (дискретизации) значений внутренней энергии вещества и, следовательно, квантованности энергообмена между э/м полем и веществом. (И, как следствие последнего, квантованности энергии э/м поля (впервые высказано Эйнштейном)). В современной литературе, как правило, дается не первоначально представленный Планком вывод формулы для ρ_ν, а предложенный им же позднее "более легкий" вариант, в котором квантуется, в конечном счете, энергия э/м поля. Этот вывод опирается вначале на классическую электродинамику и термодинамику, но затем, для совпадения теории с экспериментом, вводится квантование энергии.

Сначала дадим общий ход вывода формулы. Э/м явления описываются уравнениями Максвелла. Используется система СГС. Как известно, в теории Максвелла принимается, что мгновенная плотность энергии э/м поля в вакууме дается выражением:

,

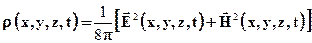где - напряженности электрического и магнитного полей. В эксперименте с "тепловыми"(хаотическими) полями измеряют средние значения энергии, поэтому усредним ρ по времени и пространству:

,

где V – объем полости, " ─ t " - усреднение по времени, T – температура стенок полости. Считается, что эта величина может быть представлена интегралом по частотам

,

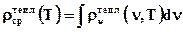где - спектральная плотность теплового излучения. Здесь dν – количество э/м энергии в единице объема полости и в полосе частот dν около частоты ν. Для малого, но конечного интервала частот ∆ν имеем

≈

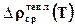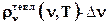
Сначала, используя уравнения Максвелла, получают наиболее общее решение для поля внутри полости, находят ρ_ν(ν,Т) и, в дальнейшем, требуют совпадения с экспериментальным значением . При этом, как указывалось ранее, имеется свобода в выборе формы полости и материала стенок. Выберем полость в форме параллелепипеда, что упрощает вид дифференциальных уравнений при покоординатной форме записи уравнений Максвелла и поиск их решений. Если в качестве материала стенок выбрать реальный материал, то не представляется возможным получить наиболее общее решение для поля в полости, так как поля проникают внутрь стенок и в принципе могут быть отличны от нуля всюду, кроме бесконечности, то есть задача становится "открытой" и, следовательно, очень сложной. Если же считать стенки идеальным металлом, то можно получить строгие решения уравнений Максвелла для свободного (без источников) э/м в полости и записать наиболее общее решение. При этом, однако, возникает следующая трудность: из-за идеальности внутренней поверхности стенок, последние полностью отражают любое падающее на них излучение и, следовательно, отсутствует энергообмен между излучением в полости и тепловой энергией в объеме стенок. То есть, ни о каком термодинамическом равновесии говорить не приходится. Эта трудность обходится так.

Прежде всего оказывается, что отличные от нуля решения уравнений Максвелла внутри полости с идеальными стенками возможны не на любой частоте, а на дискретном спектре частот, сгущающихся к бесконечности (рис.). Эти частоты естественно назвать резонансными, а полость, соответственно, резонатором, так как только на этих частотах могут быть отличны от нуля (и произвольны по значению) амплитуды полей внутри полости, а на всех остальных частотах амплитуды равны нулю. Тогда, если обозначить число резонансных частот в полосе (ν,ν+∆ν), приходящихся на единицу объема через

,

можно, для большого значения частоты ν (там, где спектр достаточно сильно сгустился и, значит, приближается к непрерывному, как у теплового излучения), потребовать выполнения равенства

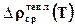≈ N ∙ ε_ср

где ε_ср – среднее значение энергии, приходящейся на одну резонансную частоту

около частоты ν для теплового равновесия при температуре Т. При этом N находится из решения электродинамической задачи для полости, а ε_ср, после доказательства эквивалентности поля в полости механической системе, – из термодинамики и статистики Больцмана для механической системы в тепловом равновесии при температуре Т. И, окончательно, спектральная плотность теплового излучения определяется из выражения

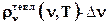= N ∙ ε_ср в виде 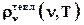= N ∙ ε_ср /

 

Теперь вывод. Найдем решения уравнений Максвелла для вакуума внутри полости с идеальными проводящими стенками при отсутствии сторонних токов и зарядов.

 

,

 

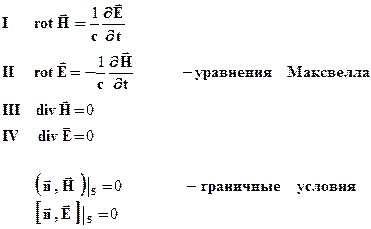где S – внутренняя поверхность параллелепипеда, 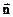- нормаль к S.

Граничные условия для Е требуют равенства нулю тангенциальной составляющей

на поверхности стенок: в противном случае были бы бесконечно большие поверхностные токи в идеальном металле и, как следствие, бесконечно большие значения напряженности магнитного поля на поверхности металла и, значит, бесконечно большая плотность энергии э/м поля, что неприемлемо (т.к. становится бессмысленным закон сохранения энергии). По этой же причине должна отсутствовать нормальная составляющая Н к поверхности идеального металла: в противном случае данная, переменная во времени, компонента Н привела бы к появлению отличной от нуля тангенциальной компоненты электрического поля, что неприемлемо по предыдущему рассуждению.

Исходная система уравнений, которую предстоит решать, не очень удобна: в ней в каждом из первых двух уравнений содержатся обе искомые функции Е и Н, и только оставшиеся 4 уравнения записаны отдельно для Е или для Н. Хотелось бы иметь систему уравнений, в которой Е и Н были "максимально" разделены, чтобы решить сначала уравнения, содержащие Е или Н, а затем – остальные. Поэтому обычно систему уравнений преобразуют в "указанном направлении" так. Из первого и второго уравнений исключим Н и выпишем новую систему уравнений:

 

 

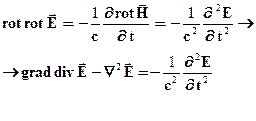
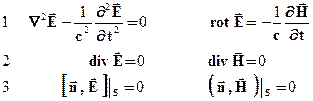
Исходная и данная системы содержат по 6 уравнений, 5 из которых совпадают. Данная система уравнений эквивалентна (но не совсем) предыдущей (исходной) в том смысле, что всякое решение исходной системы, если оно дважды дифференцируемо по пространственным и временной переменным, будет решением данной системы (видно по построению данной системы). Всякое же решение последней системы воспроизводит I-е уравнение исходной с точностью до некоторой функции, зависящей только от пространственных переменных. И если эта функция равна нулю, то решение удовлетворяет обеим системам. Поэтому, после получения решения данной системы, надо проверить удовлетворяет ли оно I-му уравнению исходной системы.

Процедура нахождения решений последней системы такова. Сначала надо найти как можно больше решений уравнений (1),(2),(3)(эти уравнения зависят только от одной искомой функции Е - это основное достоинство этой системы). Затем для каждого решения для Е интегрированием по времени rotE находим Н из уравнения, связывающего Е и Н, и проверяем, удовлетворяет ли оно двум оставшимся уравнениям для Н. Если удовлетворяет, то решение этой системы найдено и надо проверить его на удовлетворение I-го уравнения исходной системы. Затем из всех решений, удовлетворяющих указанной выше процедуре, строят общее решение, образуя суперпозицию с произвольными коэффициентами из найденных решений.

Итак, приступим к нахождению решений системы уравнений (1),(2),(3). Сначала найдем решения уравнения (1). Это волновое уравнение и время в него не входит явно. Поэтому "проходит" метод разделения временной и пространственных переменных. Ищем решение в виде:

,

то есть, вместо искомой функции Е будем искать функции U и A. Подставляем выражение для Е в уравнение (1) последней системы, имеем:

 

 

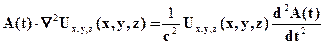
Делим это уравнение на произведение U_x,y,z(x,y,z) ∙ A(t), получаем

 

 

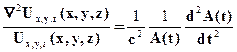
В этом уравнении левая часть зависит только от пространственных переменных, а правая - от времени. Но равенство должно выполняться для всех внутренних точек полости во все моменты времени (где U_x,y,z(x,y,z) ∙ A(t) ≠ 0). Тогда это возможно, если каждая из частей равна одной и той же константе. Т.е. :

 

 

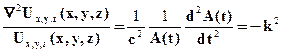
Здесь "k" – т.н. константа разделения. Знак минус определяет отсутствие нарастающих решений при t стремящемся к "+" или "-" бесконечности, т.к. нет ни источников э/м полей, ни поглощающих сред. Из последнего выражения запишем уравнение для А(t) :

 

 

Это уравнение осциллятора. Его общее решение имеет вид:

 

 

Для U_x,y,z(x,y,z) имеем уравнения:

 

 

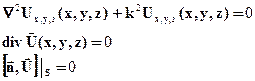
Первое уравнение – уравнение Гельмгольца. Последние два уравнения следуют из (2) и (3). Ищем решение первого уравнения методом разделения переменных на тех же основаниях, что и ранее:

 

 

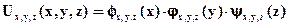
После подстановки этого выражения в уравнение Гельмгольца и разделения всех трех пространственных переменных, появятся три константы разделения k_x,k_y,k_z(также как это получалось выше при разделении временной и пространственных переменных). При этом окажется, что константы разделения удовлетворяют равенству k_x²+ k_y²+ k_z² = k², а функции Ф_x,y,z(x),φ_x,y,z(y),Ψ_x,y,z(z) - дифференциальному уравнению осциллятора (каждая по своему переменному) с "пространственной" частотой k_x, k_y, k_z соответственно. Решениями этих уравнений являются гармонические функции с произвольными амплитудами и фазами. Если потребовать, чтобы удовлетворялись граничные условия для U_x,y,z , то 6-ть из 9-ти функций Ф_x,y,z(x),φ_x,y,z(y),Ψ_x,y,z(z) определятся как sin (k_xx),

sin (k_yy), sin (k_zz) с нулевыми фазами и одновременно определятся возможные значения k_x, k_y, k_z в виде: k_x = lπ/a, k_y = mπ/b, k_z = nπ/L, где l,m,n – произвольные целые числа. Чтобы выполнялось уравнение divŪ = 0, оставшиеся три функции должны быть выбраны как cos (k_xx), cos (k_yy), cos (k_zz) c нулевыми фазами и одновременно появляется линейная зависимость между тремя амплитудными множителями в выражениях для U_x, U_y, U_z (то есть два из них остаются произвольными, а третий линейно выражается через них). Таким образом, получается, что "k", а значит и "ω", принимают дискретные значения:

 

 

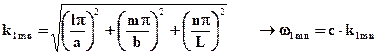
Тогда, окончательно, возможные решения для Е имеют вид:

 

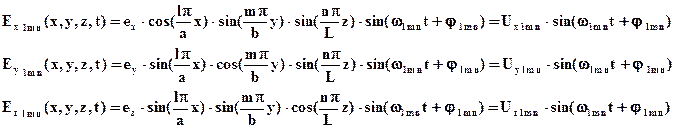
В этих выражениях два из трех амплитудных множителей e_x, e_y, e_z произвольны, а один определяется линейной комбинацией от них (об этом говорилось выше) из уравнения:

 

 

Если для произвольных l,m,n, используя выражение для Е, из уравнения, связывающего Е и Н, найти Н, то уравнение divH = 0 и граничные условия для Н выполняются "автоматически", а также удовлетворяется уравнение I исходной системы. Т.о., задание тройки целых чисел определяет возможные решения уравнений Максвелла внутри параллелепипеда с идеальными стенками. Эта тройка с точностью до двух произвольных констант (напр., e_x и e_y, а e_z находится через них из последнего уравнения) и фазы φ_{l m n} однозначно определяет структуру поля, т.е. мгновенные значения векторов напряженностей электрического и магнитного полей в любой точке полости в любой момент времени. Эта структура называется еще модой резонатора поскольку задание (l,m,n) однозначно определяет частоту колебаний ω_{l m n} векторов Е и Н с отличной от нуля амплитудой (амплитуда может быть произвольной), а на частотах ω ≠ ω_{l m n} колебания отсутствуют, т.е. амплитуда колебаний равна нулю. Поэтому частоты ω_{l m n} называются резонансными, а полость – резонатором. Для полей моды естественна запись:

 

Л2Как видно из выражений для полей моды, мода представляет собой картину стоячих волн: например, если в выражении для Е_{x l m n} зафиксировать любые две координаты (напр., x = x₀, y = y₀), то при изменении координаты z напряженность Е_{x l m n} меняется по закону стоячей волны. Это позволяет интерпретировать неотрицательные значения чисел l,m,n как числа полуволн в распределении амплитуды поля вдоль соответствующей координаты. Следует заметить, что появление отрицательных одного или двух из чисел l,m,n приведет к смене знака в двух компонентах поля Е, что может быть учтено изменением знаков двух амплитудных множителей, а изменение знаков у всей тройки вообще не приведет к изменению в распределении поля. Избыточность отрицательных значений среди чисел l,m,n подтверждается еще и тем, что произведение трех гармонических функций, фигурирующих в выражении любой компоненты поля

, при неотрицательных l,m,n составляет полный набор функций, по которому может быть разложена любая непрерывная функция (на самом деле требования еще менее жесткие) внутри параллелепипеда. Это позволяет рассматривать только неотрицательные значения чисел l,m,n.

Обратим внимание на следующее. При фиксации набора (l,m,n), пользуясь свободой выбора двух произвольных амплитудных множителей (напр. e_x и e_y), могут быть получены две структуры полей и 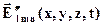(им отвечают определенные наборы амплитудных множителей (e׳_x, e׳_y) и (e^״_x, e^״_y) и, соответственно, 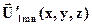и 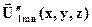), векторы напряженностей полей которых ни в одной точке полости неколлинеарны друг другу (напр., если выбрать e׳_x∙ e^״_y ≠ e^״_x∙ e׳_y) и выполняются следующие равенства:

 

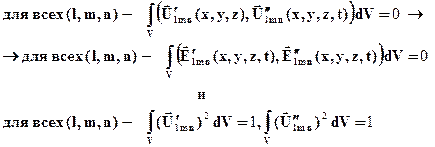
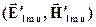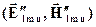Это означает, что эти поля могут быть возбуждены независимо и, следовательно, должны рассматриваться как две независимые структуры полей (две моды) на одной частоте. Поэтому общее решение уравнений Максвелла в полости на этой частоте должно быть представлено суперпозицией полей и с произвольными коэффициентами. Будем считать, что для каждой тройки (l,m,n) выбраны и зафиксированы численно наборы амплитудных множителей (e׳_{x l m n}, e׳_{y l m n}) и

(e^״_{x l m n}, e^״_{y l m n}), удовлетворяющие указанным выше свойствам. Это вполне возможно, так как множителей четыре, а на них "наложены" три равенства для U и одно неравенство для самих множителей. (При этом можно еще и выбрать любую нормировку функций U(т.е., любое число > 0 в последних двух равенствах), в том числе зависящую от (l,m,n)). Тогда можно считать, что все функци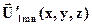и и 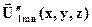определены однозначно.

Заметим, что прямой проверкой можно убедиться в правильности равенств

 

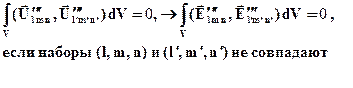
Тогда общее решение уравнений Максвелла в полости имеет вид:

 

 

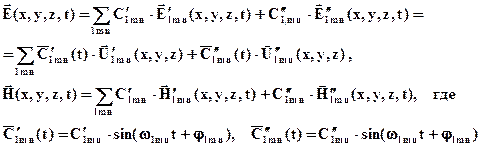
Можно показать, что заданием коэффициентов C'_{l m n} , C"_{l m n} и фаз φ_{l m n} может быть получено любое решение уравнений Максвелла в полости.

Поскольку в написанных выражениях функци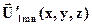и и 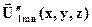полностью определены, значения напряженностей полей Е и Н в каждой точке полости и каждый момент времени однозначно определяются значением коэффициентов 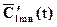, 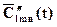(плюс аналогичные коэффициенты для Н' и Н'') в данный момент времени. (Для полей Н' и Н'', в выражениях для аналогичных коэффициентов, функции sin заменены на cos и амплитуды домножены на некоторые коэффициенты). То есть, этот бесконечный набор коэффициентов 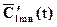, 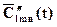плюс коэффициенты для Н' и Н'' (для всех троек l,m,n) выполняет роль обобщенных координат, численное значение которых в любой момент времени однозначно определяет состояние физической системы – свободное электромагнитное поле в полости с идеальными стенками. Как видим, 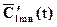,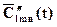плюс коэффициенты для Н' и Н'' меняются во времени по гармоническому закону с частотой ω_{l m n} , то есть функция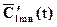(аналогично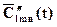и коэффициенты для Н' и Н'') удовлетворяет уравнению свободных колебаний осциллятора с частотой ω_{l m n} и представляет его общее решение. Таким образом, существует эквивалентность между свободным э/м полем в полости с идеальными стенками и бесконечным набором свободных (без внешнего воздействия) осцилляторов с частотами ω_{l m n}(по два осциллятора на каждую частоту): состояния этих систем задаются одним и тем же набором обобщенных координат, которые при одинаковых начальных условиях одинаково меняются во времени, определяя одну и ту же динамику обобщенных координат этих систем. Эта эквивалентность позволит вычислить ε_ср, так как механическая система (осциллятор – механическая система) может быть приведена в состояние термодинамического равновесия при температуре Т ( в отличие от э/м поля в полости с идеальными стенками). Например, можно поместить осцилляторы (возьмем конечное их число и будем говорить об эквивалентности между полем и осцилляторами в конечной полосе частот) в полость, стенки которой поддерживаются при температуре Т. Для некоторого упрощения картины можно потребовать, чтобы осцилляторы непосредственно не взаимодействовали между собой и со стенками полости, а взаимодействовали только с тепловым э/м полем - они все равно придут в состояние термодинамического равновесия. Такой осциллятор можно представить себе как заряженную частичку определенной массы, прикрепленную к одному концу пружины определенной жесткости (масса частицы и жесткость пружины определят собственную частоту колебаний осциллятора). Другой конец пружины надо прикрепить к какой-либо точке пространства внутри полости. Этот осциллятор будет совершать вынужденные колебания на всех частотах под действием электрической компоненты теплового излучения. Одновременно он будет излучать э/м волны (всякая заряженная частица, движущаяся с ускорением, будет излучать э/м волны). Через некоторое время после начала эксперимента такие осцилляторы "прийдут" в состояние равновесия с тепловым полем: сколько энергии в единицу времени они поглощают у поля, столько же и излучают за то же время. При этом установится некоторое постоянное среднее значение внутренней энергии осциллятора (кинетическая плюс потенциальная энергии), которая будет однозначно связана с ,где ν – собственная частота осциллятора (имеется в виду, что ν = ν_{l m n} = ω_{l m n}/2π). Можно представить себе и другие осцилляторы, и другие механизмы взаимодействия, и не с э/м полем.

Когда модель осцилляторов выбрана, подбором коэффициентов e׳_{x l m n}, e׳_{y l m n}, e^״_{x l m n}, e^״_{y l m n} можно добиться равенства между средним значением э/м энергии решения в полости с идеальными стенками на частоте ν_{l m n} и средним значением механической энергии эквивалентных им осцилляторов, находящихся в состоянии термодинамического равновесия при температуре Т. Затем, после нахождения N, определяется из приведенного в первой лекции выражения.

Перейдем к подсчету N. Надо найти число троек (l,m,n), для которых удовлетворяется неравенство: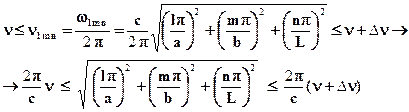

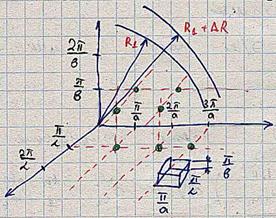
Обычно этот расчет проводят геометрически поскольку выражение с квадратным корнем похоже на выражение для расстояния от точки с координатами (lπ/а, mπ/b, nπ/L) до начала координат в прямоугольной системе координат. Введем прямоугольную систему координат, в которой на осях x, y, z отложены отрезки длиной lπ/а, mπ/b, nπ/L соответственно (рис.). Если отметить все точки с координатами (lπ/а, mπ/b, nπ/L), где (l,m,n) – неотрицательные целые числа, и построить около каждой точки параллелепипед со сторонами π/а, π/b, π/L так, что точка оказывается в его центре, то параллелепипеды плотно"замостят" область (x ≥ 0, y ≥ 0, z ≥ 0) (правда они немного будут выходить за эту область, но этим можно пренебречь при подсчете N). Построим две сферы с радиусами R = 2π∙ν/с и (R+∆R) = 2π∙(ν+∆ν)/с с центром в начале координат (на рис. R обозначено как R₁). Определим приближенно N как отношение одной восьмой объема между сферами к объему элементарного параллелепипеда, которым "замостили" область:

 

,

 

где V = abL – объем полости. Эта формула тем точнее, чем лучше выполнены неравенства ∆R 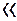R → ∆ν/ν 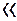1 и N 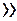1. Из формулы для N и условия N 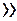1 следует:

 

, λ = с/ν

 

Оба неравенства вполне могут быть выполнены одновременно, если (λ /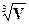) 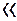1 в той же степени, что и ∆ν/ν (заметим, что при ∆ν/ν 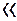1 выполняется ∆ν/ν ≈ - ∆λ/λ).

Теперь найдем ε_ср – средняя энергия, приходящаяся на одну резонансную частоту в полосе частот ∆ν около частоты ν. Вспомним, что из эквивалентности э/м поля в полости с идеально проводящими стенками и механической системы из бесконечного числа осцилляторов, вытекало, что на одну резонансную частоту полости приходятся два осциллятора, поэтому ε_ср = 2∙ε_ср.осц.. Здесь ε_ср.осц. – среднее значение внутренней энергии осцилляторов, собственные частоты которых лежат в полосе ∆ν около частоты ν и которые находятся в состоянии термодинамического равновесия при температуре Т. При малом ∆ν будем считать, что ε_ср.осц одинакова для каждого осциллятора в этой полосе частот. Пусть термодинамика верна, тогда воспользуемся утверждением Больцмана о том, что при термодинамическом равновесии при температуре Т вероятность W_ε найти у механической системы (у нас осциллятор) значение энергии ε (ε – любое число ≥ 0) есть

 

 

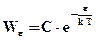
Из статистической физики для среднего значения физической величины имеем

 

ε_ср.осц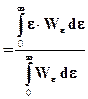

 

Беря интеграл в числителе по частям, находим ε_ср.осц = k∙T. После подстановки этого значения и выражения для N в формулу для получаем

 

 

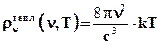
Это формула Рэлея- Джинса. Она дает хорошее совпадение с экспериментом в области низких частот и высоких температур и совершенно не верна для высоких частот. Кроме этого, если проинтегрировать по всем частотам, то, как видно из формулы, получим ∞, то есть э/м энергия в полости при конечной температуре стенок Т бесконечно велика, что не соответствует эксперименту и поэтому неприемлемо.

Чтобы получить формулу, хорошо совпадающую с экспериментом, Планк ввел предположение о том, что возможные значения внутренней энергии осциллятора не есть произвольное неотрицательное число, а есть набор дискретных чисел: 0, hν, 2∙hν, 3∙hν,..,

nhν = ε_n,… , где h – некоторая постоянная, под ν здесь понимается ν _{l m n} , то есть у каждого осциллятора свой набор возможных значений внутренней энергии (с одним и тем же, пока неизвестным, значением h !!). Теперь для расчета среднего значения внутренней энергии осциллятора надо использовать не интегралы, а суммы:

 

 

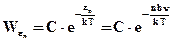
ε_ср.осц В знаменателе этого выражения стоит сумма членов ряда геометрической прогрессии и поскольку 0 < 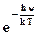< 1 эта сумма конечна и вычисляется по известной формуле:

 

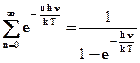Если продифференцировать правую и левую части по ν,то

можно получить выражение для числителя предыдущей формулы:

 

. Тогда ε_ср.осц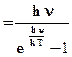

И окончательно получаем:

 

―Формула Планка

 

При h = 6,62 ∙ 10 ^-27 (эрг ∙ сек) наблюдается хорошее совпадение теории с экспериментом при всех ν и Т. h – постоянная Планка. hν – квант энергии – расстояние по энергии между соседними значениями внутренней энергии осциллятора с собственной частотой ν. Поскольку внутренняя энергия осциллятора квантована, энергообмен между э/м полем и осциллятором квантован и, как следствие этого, квантована энергия э/м поля . То есть, для любой частоты ν соседние возможные значения энергии поля этой частоты имеют разницу hν.

Найдем среднее число квантов энергии для равновесного (теплового) излучения на частоте ν:

 

ε_ср.осц / hν =

 

Для оптического диапазона (ν ~ 10¹⁴ гц) и комнатной температуры (Т = 300 К) имеем:

ε_ср.осц / hν ≈ e ^{– 40} . То есть, вероятность зарегистрировать квант энергии оптического диапазона при комнатной температуре исчезающе мала (т.е., в эксперименте этого не должно наблюдаться, что и подтверждается).

Формула Планка получена противоречивым образом: выражение для N вычислено из классической электродинамики, в которой энергия не квантуется, а среднее значение внутренней энергии осциллятора (а значит и энергия моды, эквивалентной данному осциллятору) получено в предположении ее квантованности. Это противоречие вынуждало теоретиков искать другой, непротиворечивый вывод формулы Планка. И в 1916 году Эйнштейн, опираясь на теорию атома Бора и постулировав микроскопические процессы взаимодействия атомов с э/м полем, дал непротиворечивый вывод формулы Планка. Его постулат о вынужденном излучении много позже был подтвержден созданием квантовых усилителей и генераторов: мазеров и лазеров.

 

КОЭФФИЦИЕНТЫ ЭЙНШТЕЙНА И ФОРМУЛА ПЛАНКА

 

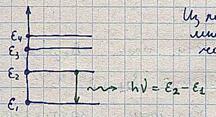В работе 1916 г., Эйнштейн, опираясь на модель атома Бора, постулировал как происходят излучательные переходы между энергетическими уровнями атома. К излучательным переходам относятся такие, при которых происходит энергообмен между внутренней энергией атома и энергией э/м поля. Между любой парой энергетических уровней, определяющих возможные значения внутренней энергии атома, молекулы и т.д., в общем случае, возможны как излучательные, так и безизлучательные переходы. При безизлучательных переходах происходит энергообмен между внутренней энергией атома и другими,"неэлектромагнитными", формами энергии, например, при столкновении атомов это может быть их кинетическая энергия. Эйнштейн постулировал три типа излучательных переходов между уровнями: самопроизвольные(спонтанные) "сверху вниз", вынужденные "сверху вниз" и "снизу вверх".

Эйнштейн использовал вероятностный язык для описания количественной стороны излучательных переходов по аналогии с тем, как описывается радиоактивный распад атомов. А именно, если атом находится в возбужденном состоянии, например, на рисунке на уровне m, то он может самопроизвольно перейти на любой ниже расположенный уровень n с излучением кванта света с энергией hν = ε_m – ε_n (ε_m > ε_n). Вероятность этого перехода за единицу времени дается коэффициентом Эйнштейна А_{m n}. Или, если в момент времени t число атомов на уровне m есть n_m(t) (n_m называется населенностью уровня m в момент времени "t") , то число спонтанно перешедших атомов с уровня m на уровень n и, соответственно этому, число спонтанно излученных квантов за время dt, согласно постулату Эйнштейна, определяется выражением:

 

_‌‌│dn_m│ = A_{m n}∙ n_m(t)∙dt

 

Если опустить знак модуля, то справа надо поставить знак минус, а величину слева считать изменением населенности уровня " m " за время dt за счет спонтанных переходов (они уменьшают населенность уровня " m "). Постулируется, что при каждом акте спонтанного перехода "родившийся" квант может с равной вероятностью "полететь" в любом направлении и иметь произвольную поляризацию. Когда атомы можно считать независимыми, спонтанное излучение по своим характеристикам "выглядит" как шум. Заметим еще, что коэффициент А_{m n} величина размерная с размерностью, обратной времени - [1/сек]. А_{m n} зависит от частоты (точнее от энергетических состояний m и n), "параметров" атома, постоянных h и c и некоторых внешних условий.

Вынужденные переходы с поглощением. Эйнштейн постулировал: если на атом, находящийся в нижнем энергетическом состоянии, падает излучение со спектральной плотностью 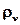, то с вероятностью 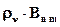за единицу времени он может перейти в верхнее энергетическое состояние с поглощением кванта энергии. При этом, по закону сохранения энергии, должно выполняться hν = ε_m – ε_n. Если ни для одной пары энергетических уровней последнее условие не выполняется то, по этой модели, излучение такой частоты не взаимодействует с атомом и поглощения нет. Коэффициент В_nm называется коэффициентом Эйнштейна для вынужденного излучения (или поглощения) и зависит от параметров атома и постоянной h. 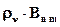- размерная величина с размерностью – 1/сек и, в соответствии с ее определением, "дает" число вынужденных переходов ε_n → ε_m с поглощением (или число поглощенных квантов) за время dt:

 

│dn_n│ = 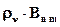∙ n_n(t)∙dt , n_n(t) – населенность уровня n в момент времени "t".

 

Оба приведенных выше перехода были известны и раньше, но Эйнштейн ввел еще один новый вынужденный переход – вынужденный переход с излучением. Если атом находится в состоянии с энергией ε_m и облучается излучением со спектральной плотностью 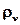, то он может совершить вынужденный переход в нижнее состояние ε_n при условии hν = ε_m – ε_n. Вероятность этого перехода за единицу времени постулируется равной 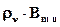. При этом излучается квант энергии э/м поля hν. Это так называемое вынужденное излучение. Оно появляется при наличии вынуждающего излучения, которое на этот акт энергию не затрачивает – достаточно его присутствия в месте, где расположен атом. По своим характеристикам (направление распространения и поляризация) вынужденное излучение полностью тождественно вынуждающему излучению. Если условие hν = ε_m – ε_n не выполняется, то вынужденного излучения (равно как и вынужденного поглощения) нет, то есть вынужденные переходы с поглощением или с излучением носят резонансный характер. Поэтому имеет смысл выделять резонансные частоты и для них писать нижние индексы: ν_{m n} . ν_{m n} часто называют частотой перехода. Если в момент времени "t" населенность верхнего уровня есть n_m(t), то число вынужденных переходов с излучением и, соответственно, число вынужденно излученных квантов за время dt дается выражением:

 

│dn_m│ = 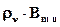∙ n_m(t)∙dt

 

Все свойства спонтанных и вынужденных переходов постулированы Эйнштейном и в дальнейшем подтвердились экспериментально. Следует заметить, что эти постулаты были введены Эйнштейном для вывода формулы Планка, а поэтому соответствуют условиям взаимодействия атомов с тепловым излучением. То есть правильнее было бы в постулатах Эйнштейна о вынужденных переходах писать не просто 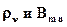, а 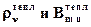. Однако, в литературе так не пишут, но это надо иметь в виду.

 

Л3 Теперь вывод Эйнштейном формулы Планка. Пусть имеется "большое" множество (чтобы использовать статистические закономерности) одинаковых атомов. У каждого атома одинаковый набор энергетических уровней, показанных на рисунке. Пусть атомы помещены в полость с равновесным тепловым излучением. Будем считать, что атомы не взаимодействуют друг с другом и со стенками полости, а взаимодействуют только с тепловым излучением. Поэтому любые переходы между энергетическими уровнями будут только излучательными и описываются постулатами Эйнштейна. Если тепловое излучение подчиняется термодинамическим закономерностям (считаем, что это так), то совокупность атомов придет в состояние термодинамического равновесия. Поскольку это - равновесие, то внутренняя энергия всей совокупности атомов, в среднем, должна оставаться постоянной во времени. Внутренняя энергия невзаимодействующих друг с другом атомов, естественно, дается суммой по всем "i": ∑ ε_i∙ n_i . Откуда следует, что в равновесии остаются постоянными средние по времени значения населенностей уровней n_i. Но это равновесие динамическое и, значит, за счет взаимодействия с тепловым излучением, осуществляются переходы атомов между энергетическими уровнями. Самое простое, чтобы не менялись населенности уровней, предположить, что выполняется принцип детального равновесия: для любой пары уровней m и n число переходов "m → n" за единицу времени равно числу переходов "n → m" за то же время. Тогда, учитывая, что "сверху вниз" идут спонтанные и вынужденные переходы, а "снизу вверх" – только вынужденные, имеем равенство для единицы времени:

 

,

 

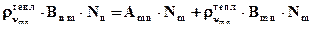где введены обозначения N_m , N_n – населенности уровней при термодинамическом равновесии. Из последнего равенства следует:

 

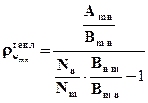Из принципа Больцмана следует, что при термодинамическом равновесии при температуре Т вероятность W_n найти у механической системы значение энергии ε_n есть:

 

W_n ~ g_n∙=> => ,

где g_n – кратность вырождения уровня энергии ε_n , то есть число различных пространственных конфигураций электронного облака, соответствующих одному значению энергии (в данном случае ε_n). При записи этого выражения использовалось естественное соотношение N_n = W_n∙N₀ и аналогично для N_m, где N₀ - полное число частиц.

Из разумных соображений понятно, что при Т, стремящемся к ∞, должно и стремиться к ∞, откуда следует равенство . При малых Т и больших ν экспериментальная кривая для хорошо описывается формулой Вина:

~ (α – некоторая константа). Сравнивая эту формулу с последней формулой вывода (при учете ε_m – ε_n » kT), имеем: ε_m – ε_n = k∙α∙ν = h∙ν_{m n},(здесь h - константа, равная k∙α). Тогда

 

. При больших Т и малых ν экспериментальная кривая для хорошо описывается формулой Рэлея – Джинса: . Сравнивая эту формулу с предыдущей (при условии h∙ν_{m n} « kT) получаем: ν = ν_{m n} и .

Если считать здесь h равной постоянной Планка, то окончательно получаем формулу:

 

. То есть, на всех частотах ν = ν_{m n} , соответствующих всем частотам переходов для данного типа атомов, имеем совпадение с формулой Планка. Ясно, что для других атомов, получилось бы совпадение с формулой Планка для другого бесконечного набора частот и так далее. Поэтому в формуле для можно опустить нижние индексы у частоты и считать верной эту формулу для всех частот ν. Тогда последняя формула совпадет с формулой Планка.

Обратим внимание на то, что отношение коэффициентов Эйнштейна А_{m n} к В_{m n} зависит только от частоты. Следовательно, для любой частоты ν_{m n} , с ростом температуры растет вероятность вынужденных переходов между уровнями энергии атома, находящегося в "тепловом поле" (из-за роста (ν_{m n} ,T) ), а вероятность спонтанных переходов не меняется. Таким образом, доля вынужденного излучения в "тепловом излучении" растет с ростом температуры.

Решим несколько задач с использованием коэффициентов Эйнштейна. Но прежде нам понадобится понятие двухуровневой системы.

 

ДВУХУРОВНЕВАЯ СИСТЕМА

 

Многие задачи на взаимодействие излучения с веществом решаются легче, если у атомной системы учитываются только два энергетических уровня. Это допустимо, если выполнены следующие два условия: 1- выделенная пара уровней по разности энергий не должна совпадать ни с одной другой парой (иначе, из-за "резонансности" взаимодействия излучения с атомами, нельзя было бы ограничиться одной "парой" уровней); 2 – не должно быть переходов между выделенными и другими уровнями и необходимо, чтобы выполнялось n_m+n_n = const. Такие системы называются двухуровневыми. Аналогично могут быть определены и многоуровневые системы.

 

ШУМОВАЯ ТЕМПЕРАТУРА СПОНТАННОГО ИЗЛУЧЕНИЯ

 

 

Данный параметр характеризует шумовые свойства квантовых усилителей. На рисунке приведена общая качественная схема квантового усилителя. На вход волноведущей системы поступает подлежащий усилению сигнал. Внутри волновода находится рабочее вещество (считаем его состоящим из двухуровневых атомов) в состоянии, при котором оно способно усиливать проходящий через него сигнал. На выходе усилителя присутствует не только усиленный сигнал, но и шумы. Мощность шумов складывается из теплового излучения стенок волновода и спонтанного излучения рабочего вещества. Для сравнения этих двух видов шумов желательно, чтобы они определялись одинаковым физическим параметром, который, хотя бы в одном из этих случаев, указывал бы на причину шума. Мощность теплового излучения стенок волновода связана с температурой стенок Т₀ и может ею характеризоваться. Естественно найти параметр с размерностью температуры, который бы аналогичным образом был связан с мощностью спонтанного излучения. Это и есть эквивалентная шумовая температура спонтанного излучения Т_ш.сп.. Она вводится следующим образом. Если вероятность в единицу времени спонтанного излучения атома, находящегося в верхнем энергетическом состоянии, равна А₂₁, то какова должна быть температура черного тела, окружающего атом в нижнем энергетическом состоянии, для того, чтобы его вероятность индуцированного поглощения в единицу времени также равнялась А₂₁. При этой температуре окружающее черное тело будет излучать шумы, эквивалентные спонтанному излучению атома. (Черное тело это идеализированный объект, который поглощает все падающее на него излучение, а, следовательно, при тепловом равновесии, столько же и излучает.) В соответствии со сказанным, имеем:

 

 

 

Как видим, Т_ш.сп зависит, кроме универсальных постоянных, только от частоты. Для радиодиапазона ν ~ 10¹⁰ гц, имеем Т_ш.сп ~ 1К. Отсюда следует, что если температура стенок волновода Т₀ = 300К, то спонтанное излучение можно не учитывать в сравнении с тепловым излучением стенок волновода. А при Т₀ = 4К в мощность шумов на выходе усилителя сравнимый вклад будут вносить и тепловое излучение стенок волновода, и спонтанное излучение рабочего вещества, так как Т₀ и Т_ш.сп одного порядка. Заметим еще раз, что все сказанное верно только для радиодиапазона, где Т_ш.сп ~ 1К.

 

РЕЛАКСАЦИИ

 

Возвращение системы в состояние равновесия после снятия возмущения, которое вывело ее из равновесия, называется релаксацией. Опишем динамику релаксации двухуровневой системы. Пусть есть двухуровневая система (рис.). Пусть возвращение системы в состояние равновесия описывается вероятностью Р₁₂ перехода в единицу времени для одной частицы из состояния 1 в 2 и вероятностью Р₂₁ - из 2 в 1 (эти вероятности в общем случае учитывают и излучательные и безизлучательные переходы и зависят как от свойств самих атомов, так и от свойств окружающей их среды). Обозначим через N₀, N₁ и N₂ полное число частиц и населенности 1 и 2 уровней в состоянии термодинамического равновесия. Тогда при термодинамическом равновесии должно быть равенство числа переходящих частиц из 1 в 2 числу переходящих из 2 в 1 за единицу времени, т.е.:

 

Р₁₂∙ N₁ = Р₂₁∙N₂ →

В написанной формуле появление экспоненты такое же, как и при выводе Эйнштейном формулы Планка.

Внесение возмущения приводит к изменению населенностей уровней. После снятия возмущения населенности уровней "релаксируют"(изменяются) к равновесным значениям. Обозначим текущие значения населенностей через n₁(t) и n₂(t), которые удовлетворяют естественному равенству:

n₁(t) + n₂(t) = N₁+N₂ = N₀

Напомним, что под изменением населенности уровня за время dt понимают dn(t) = n(t+dt) – n(t). Используя определение вероятностей, запишем изменение населенности второго уровня за время dt : dn₂(t) = P₁₂∙n₁(t)∙dt – P₂₁∙n₂(t)∙dt . Знаки плюс и минус у первого и второго слагаемого связаны с тем, что первое слагаемое описывает переходы 1→ 2, которые увеличивают населенность второго уровня, а второе слагаемое описывает переходы 2→ 1, которые уменьшают населенность второго уровня. Выпишем оба уравнения вместе:

n₁(t) + n₂(t) = N₀

dn₂(t)/dt = P₁₂∙n₁(t) – P₂₁∙n₂(t)

Из этих уравнений нетрудно найти n₁ и n₂ как функции времени. Однако в литературе чаще пользуются другими переменными: ∆n = n₂(t)-n₁(t) - инверсная населенность уровней и N₀. Легко получить:

n₂(t) = 1/2∙(∆n + N₀ ), n₁(t) = 1/2∙( N₀ - ∆n)

После подстановки этих выражений во второе уравнение системы получим:

 

После несложных преобразований можно получить уравнение:

 

, где ∆N = N₂ – N₁, - время релаксации.

Из уравнения видно:

1. Скорость изменения инверсии (d(∆n)/dt) прямо пропорциональна отличию инверсии ∆n от равновесной инверсии ∆N;

2. Если ∆n = ∆N , то, как следует из уравнения, ∆n = const.

 

Общее решение уравнения есть:

 

, где С – начальная инверсная населенность.

 

РЕЗОНАНСНОЕ ПОГЛОЩЕНИЕ ИЗЛУЧЕНИЯ ВЕЩЕСТВОМ

 

Разберем еще одну задачу, которая допускает решение с использованием постулатов Эйнштейна. Пусть проводится эксперимент, представленный на рисунке. Э/м излучение от генератора поступает в волновод, заполненный веществом. Дошедшая до конца волновода э/м мощность измеряется измерителем мощности.

 

 

На рис. представлена типичная зависимость мощности генератора (Р_ген.) и мощности, измеренной измерителем мощности, (Р_изм.) от частоты в некоторой полосе частот в присутствии вещества и без него. На левом рисунке отличие Р_ген от Р_изм связано с поглощением э/м излучения в стенках волновода (из-за их конечной проводимости). На правом рисунке для всех частот кроме частоты ν₀ и небольшой окрестности около нее все совпадает с левым рисунком. Отличие зависимостей естественно связать с присутствием вещества, которое, как видим, привносит дополнительное к "волноводному" поглощение на частоте ν₀ и в небольшой окрестности около нее. Если, в первом приближении, считать окрестность бесконечно узкой, то объяснение дополнительного поглощения на частоте ν₀ может быть связано с существованием у атомов вещества среди множества энергетических уровней такой пары, расстояние между которыми равно һν₀, то есть ε₂ – ε₁ = һν₀ . С учетом всего сказанного, для ν ≠ ν₀, поглощение мощности э/м излучения при прохождении слоя dx около координаты "х" можно представить как:

dP(x) = -α_волн.∙ P(x)dx, где α_волн – коэффициент поглощения излучения стенками волновода на единицу длины (считаем для простоты, что в выбранном диапазоне этот коэффициент не зависит от частоты). Эта формула приводит к хорошо известному в оптике и подтвержденному экспериментально закону Бугера:

P(x) = P(0)∙

Для ν = ν₀ необходимо учесть, что присутствует и поглощение излучения стенками волновода и изменение мощности излучения за счет взаимодействия с веществом. Будем считать выполненными условия для двухуровневой системы и верными постулаты Эйнштейна для излучательных переходов. Пусть для одного атома за единицу времени вероятность вынужденных переходов между уровнями 1 и 2 под действием монохроматического излучения спектральной плотности ρ есть Вρ (здесь ρ зависит от x; считаем, что В₁₂ = В₂₁ = В; при этом нужно иметь в виду, что численные значения этих коэффициентов отличаются от аналогичных коэффициентов Эйнштейна, которые описывают вынужденные переходы атомов под действием теплового, а не монохроматического излучения как в данном примере). Обозначим населенности уровней в расчете на единицу длины вещества через n₁, n₂, тогда число переходов с поглощением в слое dx за единицу времени есть n₁Вρ(x)dx и, соответственно, поглощаемая мощность - һν₀∙n₁Вρ(x)dx, а мощность, излученная веществом слоя, представится выражением һν₀∙n₂Вρ(x)dx. В последнем выражении не учтены спонтанные переходы в предположении, что выполняется А₂₁ « Вρ (здесь А₂₁ – вероятность спонтанных переходов). Тогда изменение мощности излучения при прохождении слоя dx будет:

dP(x) = -α_волн.∙ P(x)dx - һν₀∙( n₁ - n₂)Вρ(x)dx = -(α_волн. + γ В∙( n₁ - n₂)) P(x)dx ,

где в коэффициенте γ учтено, что ρ(x) ~ P(x).

Отсюда новый коэффициент поглощения α будет:

α = α_волн. + γ В∙( n₁ - n₂)

Л4 Естественно считать коэффициентом поглощения вещества на единицу длины величину γ В∙( n₁ - n₂). Видим, что если n₁ > n₂ , то вещество поглощает часть проходящего через него излучения (заметим, это только при ν = ν₀) и α > α_волн . Как известно, такое соотношение населенностей уровней (n₁ > n₂) наблюдается, в частности, при термодинамическом равновесии. Наличие в веществе "стороннего" излучения выводит его из состояния термодинамического равновесия и новые равновесные значения населенностей уровней отличаются от прежних: населенность нижнего уровня уменьшится, а верхнего возрастет. Однако, если мощность "стороннего" излучения не очень велика, изменение населенностей можно не учитывать. С учетом этого получим выражение для коэффициента поглощения вещества. Итак, пусть в присутствии э/м излучения от генератора выполняется

n₁ ≈ N₁

n₂ ≈ N₂, где N₁, N₂ – населенности уровней в состоянии термодинамического равновесия. Согласно теореме Больцмана, для термодинамического равновесия имеем:

. Если hν₀ « kT₀, то из предыдущей формулы следует _.

Поэтому: n₁ - n₂ ≈ N₁- N₂ = N₁( 1 - ) ≈ N₁≈ , где N₀ = N₁ +N₂ и еще раз учтено, что hν₀ « kT₀.

Тогда коэффициент поглощения излучения в волноводе с веществом на частоте ν₀ на единицу длины имеет вид:

α = α_волн. + γ В∙. Эта явная зависимость коэффициента поглощения от N₀, ν₀, Т₀ и некоторых характеристик атомов (входят в В) легко может быть подтверждена экспериментально.

 

КВАНТОВОЕ УСИЛЕНИЕ И ЭФФЕКТИВНАЯ

ОТРИЦАТЕЛЬНАЯ ТЕМПЕРАТУРА