Модель Бертрана для дифференцированного продукта

Рис. 1. Матрица выигрышей игрока

Рис. 1. Матрица выигрышей заключенных

 

Для каждого из них домини­рующей стратегией или стратегией, приносящей наибольший выигрыш при любой стратегии другого игрока, является стратегия «сознаваться». Каждый заключенный думает, что другой признается первым и обречет его на более суровое наказание. Рациональный выбор обоих будет состоять в том, чтобы сознать­ся, несмотря на возможность улучшить положения обоих при выборе ими стратегии «не сознаваться».

Подобным образом не доверяют друг другу и фирмы. Они также как и заключенные не могут принудить друг друга к выполнению достигнутых договоренностей. Рассмотрим пример стратегического взаимодействия фирм по цене. Возмож­ные комбинации их стратегий и получаемых ими выигрышей пред­ставлены в виде матрицы выигрышей на рис.2.

	Стратегии фирмы 2
Низкая цена: 5	Высокая цена: 10
Стратегии фирмы 1	Низкая цена: 5	(2; 2)	(4; 1)
Высокая цена: 10	(1; 4)	(3; 3)

 

В однопериодной игре доминирующей стратегией для каждой фир­мы будет стратегия «назначать низкую цену». Равновесие рынка с низкими ценами будет служить равновесием по Нэшу (американский математик Джон Нэш) в не­повторяющейся игре.

Равновесие по Нэшу – это такое состояние рынка, при котором каждое предприятие придерживается стратегии, являющейся наилучшим ответом на стратегии других конкурентов. То есть ни одно предприятие не хочет изменить своего поведения в одностороннем порядке.

Если игра или стратегическое взаимодействие фирм продолжается бесконечно долго, то доминирующими будут, по крайней мере, две стра­тегии:

1. Стратегия «руки, дрожащей на курке» - назначить высокую цену в момент t, если другая фирма назначила высокую цену в момент (t-1) и наоборот.

2. Стратегия «хищничества» - назначать низкую цену в любой момент времени.

Максимальный выигрыш каждой фирмы от первой стратегии, получаемой в бесконечном периоде, который приведен к текущему моменту времени:

(2)

где 3 - прибыль при цене 10 руб./ед. прод., если другая фирма установит эту же цену;

d - дисконтирующий множитель: d = l/(l+i), i - процентная ставка;

r - вероятность вза­имодействия фирм в следующем периоде (t+1).

Если фирма 2 установит цену 5 в первом периоде, то цена фирмы 1 во втором периоде тоже будет 5, максимальный выигрыш фирмы от применения стратегии низкой цены равен:

(3)

 

где 4 - прибыль, полученная фирмой 2 при цене 5, при условии, что фирма 1 назначает цену 10;

2 - прибыль фирмы 2 при цен 5, при условии, что фирма 1 назначит цену 5 начиная со второго периода.

Следовательно, выбор оптимальной стратегии фирмы, зависит от наибольшей величины выигрыша.

 

Модель показывает то, что дифференциация продукта смягчает ценовую конкуренцию. При этом соперничество фирм не ведет к полному исчезно­вению их прибылей. Пусть функция спроса первого дуополиста имеет вид:

, (4)

где a1, b1, z1 – положительные константы;

при этом 0<z1<b1 и a1>с(b1-z1).

Условие z1<b1 означает, что если цены товаров обеих фирм вырас­тут на бесконечно малую величину e, объем спроса на оба товара сокра­тится. Условие a1>AC(b1-z1) означает, что если обе фирмы назначат цены на уровне предельных издержек, объемы спроса на их товары будут по­ложительными.

Естественно, что при понижении цены Р1 первый дуополист увеличит выпуск, а понижение цены конкурента, наоборот вызывает снижение выпуска первого дуополиста. Функция прибыли дуополиста имеет вид:

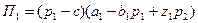, (5)

где с – затраты предприятия на единицу продукции.

Следует заметить, что при принятии дуополистами решений о ценообразовании ими будет учитываться уровень цены, установленный на предыдущем шаге. При этом в силу предпосылок модели Бертрана дуополисты принимают решения при нулевых коэффициентах вариации.

Таким образом, необходимое условие максимизации прибыли примет вид

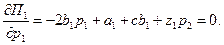(6)

Оно задаёт кривую реакции первого дуополиста:

(7)

По аналогии также можно представить функцию спроса и кривую реакции для второго дуополиста.

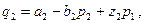
(8)