Конкуренция по Штакельбергу

Рис.1. Изопрофиты и кривые реакции фирмы 1.

Варианты стратегического поведения

На олигопольном рынке

Моделирование стратегического взаимодействия

ОТРАСЛЕВОГО РЫНКА

МОДЕЛИ СТРАТЕГИЧЕСКОГО ПОВЕДЕНИЯ СУБЪЕКТОВ

Стратегическое поведение – это такое поведение фирмы, когда при выборе варианта действия на рынке она принимает во внимание возможные ответные действия конкурентов.

Стратегическое поведение осуществляется в двух формах: в виде некооперативного и кооперативного взаимодействия.

В условиях кооперированной олигополии субъекты рынка вступают в сговор (тайный или открытый).

При некооперативном взаимодействии фирмы конкурируют и проводят самостоятельную политику на рынке.

Варианты стратегического поведения фирм зависят от:

1) последовательности принятия ими решения;

2) от выбора фирмой стратегической переменной (цены или количества).

Таблица 1

	Стратегическая переменная
Решения принимаются фирмами по объему продаж	Решения принимаются фирмами по цене
Решения принимаются	Одновременное	Модель Курно	Модель Бертрана
Последовательно	Модель Штакельберга	Модель Форхаймера

Для моделирования стратегического взаимодействия фирм применяется теория игр, представляющая собой математический аппарат для принятия оптимальных решений в конфликтных ситуациях, в которых одна сторона выигрывает за счет проигрыша другой.

Если решение выбирается в зависимости от наступления одного из вариантов окружающей действительности (природы), то такие игры являются «играми с природой».

Стратегические решения бывают чистыми и смешанными.

Чистая стратегия - это любое возможное действие какой-либо фирмы (игрока).

Смешанная стратегия – это вероятность применения каждой из множества стратегий. Она состоит в случайном выборе одной из чистых стратегий.

В настоящее время единой модели олигополии нет. Однако существует несколько общих предпосылок для всех моделей:

- убывающая кривая спроса;

- взаимозависимость производителей-продавцов товаров при принятии стратегических решений.

- олигополист не знает точные кривые спроса конкурентов.

Олигополия может быть ценовой и количественной.

Олигополия количественная - если олигополисты принимают решение об объеме выпуска продукции. Если решения принимаются по цене на продукцию, то олигополия ценовая.

В классических моделях олигополии анализируют взаимодействие фирм, максимизирующих прибыль, исходя из их рационального поведения.

Условия максимизации прибыли для количественной и ценовой олигополии различны.

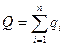Пусть на рынке олигополии конкурируют п фирм c объёмами производства q₁, q₂, ..., q_n. Объем совокупного спроса известен и задан функцией , где Прибыль каждого олигополиста зависит от структуры предложения участников рынка.

Поэтому условие максимизации прибыли предполагает выполнение равенства

(2)

При этом каждый i-й олигополист должен учитывать значения коэффициентов вариации: 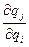(при i ¹j). Они показывают, как изменяется выпуск конкурента при изменении выпуска i-го олигополиста на единицу.

Благодаря этому при принятии решения олигополист может прогнозировать ответные действия конкурентов.

Если олигопоилст знает предполагаемые вариации, то он может выявить функциональную зависимость своего уровня выпуска от объемов конкурентов. Эти зависимости определяют кривую реакции

Кривая реакции - это наилучший ответ олигополиста на действия конкурентов, дающий максимум прибыли при конкретной комбинации продаж конкурентов.

Один и тот же уровень прибыли может достигаться при различных комбинациях объемов выпуска олигополилистов.

Множество таких комбинаций образуют изопрофиту, семейство которых олигополист рассматривает при принятии решений.

R₁(q₂) – кривая реакции фирмы 1 на изменение объема продаж фирмы 2 (q₂),

R₁(P₂) – кривая реакции фирмы 1 на изменение цены фирмы 2 (Р₂),

П^j₁ – прибыль фирмы 1 от различных комбинаций стратегических решений дуополистов по цене или количеству, которые отображаются семейством изопрофит (*).

В отличие от количественной конкуренции в ценовой кривые реакции и изопрофиты рассматриваются в n-мерном пространстве цен, а не выпусков.

Коэффициенты вариации, характеризуют изменения цены, товара каждого из конкурентов при изменении цены i-го олигополиста на определенную величину.

Изопрофитами будут множество комбинаций цен всех олигополистов, соответствующих одному и тому же уровню прибыли какого-либо олигополиста.

Кривая реакции – это множество точек, соответствующих максимальному уровню прибыли, который может получить олигополист при сложившейся комбинации цен конкурентов.

Исходные условия:

- модель дуополии, когда на рынке взаимодействуют две фирмы;

- фирмы предлагают однородный продукт;

- фирмам известна функция рыночного спроса вида

р =а-bQ,

где a, b – положительные константы,

Q – рыночный спрос, который складывается из объёмов предложения первой и второй фирм (Q = q₁+q₂) при цене Р.

- издержки производства фирм равны;

- фирмы максимизируют прибыль.

- Первой стратегический ход делает наиболее сильная фирма – «лидер», а второй – фирма – «последователь».

Прибыли дуополистов определяются как разница между выручкой и издержками каждого из них

Пi =TRi – Tci, (10)

Где Тсi – издержки производства,

ТRi – выручка фирмы;

П_i – прибыль фирмы.

Кривую рыночного спроса в линейной форме можно преобразовать

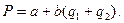(12)

В этом случае функция прибыли каждого дуополиста будет определяться как разность между выручкой получаемой им при сложившейся рыночной цене и затратами на производство реализуемой на рынке продукции.

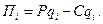(13)

Подставив в формулу 12 формулу 13 мы получим функцию прибыли для каждого дуополиста (14):

(14)

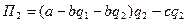
Отсюда становится возможным определять изменение прибыли дуополиста под влиянием его стратегических действий и при неизменном поведении конкурента.

Для того чтобы найти максимум прибыли дуополиста на рынке необходимо полученную формулу прировнять к нулю и продифференцировать по объёму продаж (15):

(15)

Для определения стратегического эффекта необходимо определить коэффициент вариации. При этом следует учитывать, что последователь рассматривает уровень выпуска лидера как не предсказуемый, то есть последователь принимает решение без учёта стратегического эффекта. Он максимизирует прибыль, используя кривую реакции, полученную исходя из своей функции максимума прибыли и при неизменном поведении лидера.

Для последователя кривая реакции выглядит следующим образом (16):

. (16)

Однако в отличие от последователя лидер осознаёт, что оказывает влияние на принятие его решений и поэтому учитывает реакцию последователя при решении задачи на максимум прибыли. Поскольку кривая реакции последователя известна, становится возможным определить коэффициент вариации (17):

(17)

При увеличении объёма продаж лидера на единицу, объём продаж последователя сократится на пол-единицы. Для определения стратегического эффекта требуется умножить коэффициент вариации на производную функции прибыли фирмы лидера, взятую по объёму продаж фирмы–последователя:

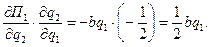(18)

После добавления стратегического эффекта в функцию максимума прибыли лидера она примет следующий вид 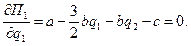(19):

(19)

Это уравнение задаёт кривую реакции фирмы–лидера, которая в результате преобразований примет вид 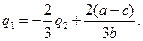(20):

(20)

Исходя из системы полученных уравнений кривых реакций, можно определить равновесные уровни выпуска дуополистов по Штакельбергу (21):

. (21)

Для подтверждения того, что фирмы получат максимум прибыли при этих объёмах продаж необходимо дважды продифференцировать функцию прибыли по объёму производства фирмы 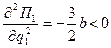(22).

, . (22)

Поскольку частные производные функции прибыли второго порядка отрицательны, можно сделать вывод о том, что равновесные объёмы выпуска обеспечивают максимум прибыли, как для дуополиста–лидера, так и для дуополиста –последователя.

При этом лидер получит прибыль в размере:

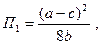(23)

а последователь получит прибыль в два раза меньше:

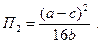(24)

Аналогичным образом моделируется стратегическое взаимодействие в условиях количественной дуополии по Курно. Однако в отличие от модели Штакельберга, в модели Курно оба дуополиста рассматривают уровень выпуска конкурента, как постоянный и при данной предпосылке принимают решение об уровне своего выпуска (не учитывается стратегический эффект).

Парадокс Бертрана и дилемма заключенного

Исходные условия:

- дуополия;

- средние издержки двух фирм равны и постоянны.

- цены фирмы устанавливают одновременно.

- функция рыночного спроса:. При этом функция спроса одного из дуополистов имеет вид:

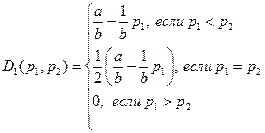(1)

- имеется рынок однородной продукции.

Каждый дуополист в целях увеличения объёма продаж будет снижать цену своей продукции на малую величину. В конечном счёте, равновесие в модели дуополии Бертрана установится в точке пересечения кривых реакции конкурентов, в которой они могут получить нулевую прибыль. В этом случае будет иметь место парадокс Бертрана.

Его суть в том, что при появлении всего одной конкурирующей фирмы рыночное равновесие может стать нестабильным и привести к «ценовой войне», а следовательно, и к конкурентному результату, то есть к нулевой прибыли в долгосрочном периоде, что нейтрализует стимулы крупных фирм к производству и сбыту данного товара.

В рамках теории игр парадокс Бертрана известен как «дилемма заключенного». Виновные в совершении преступления стоят перед выбором стратегии «сознаваться» или «не сознаваться», и делают выбор одновременно, изолированно друг от друга. При этом они не доверяют друг другу. Результаты их возможного выбора представлены на рис.1.