Метод Жордана - Гаусса
Метод Жордана-Гаусса опирается на следующее свойство систем уравнений: если к какому-либо уравнению системы прибавить любое другое уравнение системы, умноженное на некоторое число, то получится система, равносильная исходной системе уравнений. Если такое преобразование применить к системе несколько раз, то вновь полученная система уравнений также будет равносильна исходной системе.
С помощью элементарных преобразований исключим переменную  из всех уравнений, начиная со второго; затем исключим переменную
из всех уравнений, начиная со второго; затем исключим переменную  из всех уравнений, начиная с третьего, и т.д. Этот процесс называется прямым ходом и продолжается до тех пор, пока система уравнений не приобретет ступенчатого или треугольного вида. Если система совместна, то выполняется обратный ход − нахождение решений.
из всех уравнений, начиная с третьего, и т.д. Этот процесс называется прямым ходом и продолжается до тех пор, пока система уравнений не приобретет ступенчатого или треугольного вида. Если система совместна, то выполняется обратный ход − нахождение решений.
Алгоритм метода рассмотрим на конкретных примерах.
Случай 1.Решить систему уравнений:
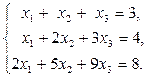
Решение. Запишем расширенную матрицу системы
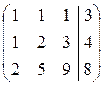
и выполним элементарные преобразования ее строк. Для этого умножим первую строку на (−1) и прибавим ко второй строке; затем умножим первую строку на (−2) и прибавим к третьей строке. В результате мы исключим переменную  из всех уравнений, кроме первого. Получим
из всех уравнений, кроме первого. Получим




 ~
~ 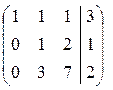 .
.
Исключим переменную 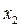 из третьего уравнения. Умножим вторую строку полученной матрицы на (−3) и прибавим к третьей строке:
из третьего уравнения. Умножим вторую строку полученной матрицы на (−3) и прибавим к третьей строке:

 ~
~ 
Прямой ход закончен. 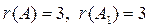 . Так как
. Так как 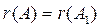 , то система уравнений совместна. Ранг матрицы системы
, то система уравнений совместна. Ранг матрицы системы  , поэтому система имеет единственное решение.
, поэтому система имеет единственное решение.
Выполним обратный ход:






 ~
~  ~
~ 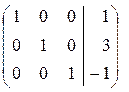 .
.
Последней матрице соответствует система уравнений 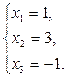
Таким образом, (1; 3;−1) − единственное решение системы уравнений.
Случай 2. Решить систему уравнений:

Решение. Запишем расширенную матрицу системы и выполним элементарные преобразования строк как в примере 1.






 ~
~  ~
~ 









 A ~
A ~  , A1 ~
, A1 ~ 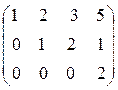 .
.
 . Итак,
. Итак,  , значит, данная система уравнений несовместна.
, значит, данная система уравнений несовместна.
Случай 3. Решить систему уравнений:

Решение. Запишем расширенную матрицу системы и выполним элементарные преобразования строк как в примере 1.










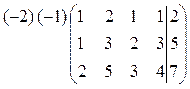 ~
~ 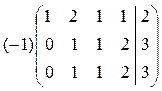 ~
~ 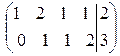 .
.
Система уравнений совместна, так как 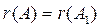 =2. Так как
=2. Так как  , то система неопределенная. Определитель, составленный из коэффициентов при переменных
, то система неопределенная. Определитель, составленный из коэффициентов при переменных  и
и  ,
,
 .
.
Поэтому переменные х1 и х2 будем считать основными, или базисными, а х3 и х4 − свободными.
Выполним обратный ход:


 ~
~ 
Запишем систему уравнений, соответствующую последней матрице:
 или
или 
Выражение основных переменных через свободные называется общим решением системы уравнений. Придавая свободным переменным произвольные числовые значения, получим частное решение системы уравнений.
Система имеет бесконечное множество решений
 .
.
 Выводы:
Выводы:
Если  , то система уравнений несовместна.
, то система уравнений несовместна.
Если 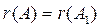 , то система уравнений совместна.
, то система уравнений совместна.
Если  , то система уравнений имеет единственное решение.
, то система уравнений имеет единственное решение.
Если  , тосистема уравнений имеет бесконечное множество
, тосистема уравнений имеет бесконечное множество
решений.