Теорема о ранге.
Ранг матрицы соответствует количеству её линейно независимых строк, или столбцов.
Вопрос № 9: Вычисление ранга матрицы методом окаймляющих миноров:
Пусть в матрице найден минор порядка к, отличный от нуля, тогда достаточно рассмотреть лишь те миноры к+1 порядка, которые содержат внутри себя, то есть окаймляют минор к-ого порядка.
Если все они равны нулю, то минор к-ого порядка – базисный минор, а ранг матрицы равен рангу базисного минора, то есть матрица – к-ого порядка, ну а если существуют миноры, не равные нулю, ранг которых больше к, то операцию поиска необходимо продолжать. к:=л+1;
Пример:
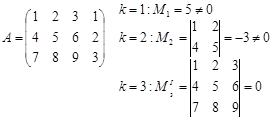
М2 – базисный минор, ранг матрицы равен двум.
Вопрос № 10: Вычисление ранга матриц методом элементарных преобразований:
Элементарные преобразования матрицы:
1. Перестановка строк, или столбцов матрицы.
2. Умножение строки, или столбцы на число, отличное от нуля.
3. Сложение строк (столбцов) матрицы.
Теорема об элементарных преобразованиях матрицы:
При элементарных преобразованиях ранг матрицы не изменяется, поэтом при помощи элементарных преобразований матрица приводится к ступенчатому, или блочно треугольному виду, по которому ранг можно определить визуально.
Пример:
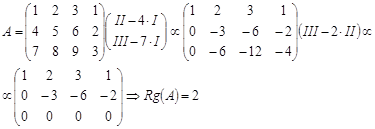
Правило определения ранга матрицы и её базисного минора:
1. Ранг ступенчатой матрицы равен количеству её не нулевых строк.
2. Базисный минор ступенчатой матрицы содержится среди элементов её не нулевых строк и такого же количества её столбцов, взятых по одному из каждой ступеньки.
Вопрос № 11: Теорема Кронекера-Капели:
1. Теорема Кронекера-Капели.
2. Общий метод решения систем из т алгебраических уравнений с п неизвестными.