Размерность линейного пространства.

Базис.

Определение.Упорядоченное множество векторов 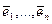образует базис пространства , если:

1) векторы 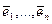линейно независимы,

2) любой вектор пространства линейно выражается через векторы .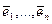

Равенство называется разложением вектора по базису 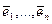. Коэффициенты называются координатами вектора в базисе .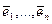

Теорема.Пусть 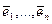- базис пространства . Тогда для любого вектора из разложение по базису единственно.

Доказательство. Пусть и . Тогда

- =,

=.

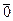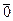Но векторы 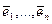линейно независимы, поэтому для всех . Теорема доказана.

Пример. В арифметическом линейном пространстве Rⁿ система векторов

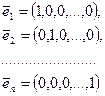
образует базис, т.к. эти векторы линейно независимы и любой вектор линейно выражается через них: .

Этот базис не единственный.

Задача.Докажите, что множество векторов

тоже образует базис.

 

Определение. Линейное пространство называется 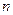-мерным, если в нем существует базис из 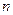векторов. Линейное пространство называется бесконечномерным, если в нем существует любое число линейно независимых векторов.

Обозначение: .

Очевидно, что в 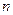-мерном пространстве любая система из векторов линейно зависима.

Вспомним некоторые примеры линейных пространств.

1).Rⁿ .

2). Пространство последовательностей бесконечномерно. Чтобы это показать, рассмотрим бесконечное множество элементов этого пространства N:

Любая конечная система таких векторов линейно независима.

 

5.5. Ранг системы векторов.Пусть - некоторое, быть может, бесконечное, множество векторов из линейного пространства . Набор векторов назовем максимальной линейно независимой системой, если эти векторы линейно независимы и добавление любого другого вектора из множества делает систему линейно зависимой. Если Х является векторным пространством, то максимальная линейно независимая система векторов в нем является базисом.

Пусть - максимальная линейно независимая система в и пусть - вектор, отличный от векторов . Тогда векторы линейно зависимы: . Заметим, что , иначе линейно зависимыми были векторы . Отсюда . Мы получили, что если - максимальная линейно независимая система, то любой вектор из линейно выражается через эти векторы. (Если вектор равен одному из векторов системы , то он очевидным образом выражается через векторы этой системы.)

Лемма. Пусть и - две системы векторов, причем векторы линейно независимы. Если векторы линейно выражаются через , то .

Доказательство. Предположим противное: пусть >. Имеем:

Рассмотрим строки, составленные из коэффициентов :

Эти строки можно считать элементами пространства R^r. Так как >, то эти строки линейно зависимы, т.е. найдутся , не все равные нулю, такие, что

.

Иначе, для . Но тогда

,

что означает линейную зависимость векторов . Значит, .

Следствие.Если и - две максимальные линейно независимые системы в , то .

Действительно, так как векторы линейно выражаются через , то . Но тоже линейно выражаются через , значит, . Отсюда .

Определение. Рангом системы векторов называется число векторов в максимальной линейно независимой системе.

Согласно только что доказанной лемме, ранг системы не зависит от выбора максимальной линейно независимой системы.