Линейная зависимость.

Определение. Линейной комбинацией векторов называется выражение

,

где R.

Замечание 1.Линейной комбинацией называется как само выражение, так и вектор, который получается в результате выполнения всех действий.

Замечание 2.Если вектор является линейной комбинацией векторов ,то говорят, что линейно выражается через .

Линейная комбинация называется тривиальной, если все коэффициенты 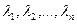равны нулю. Линейная комбинация называется нетривиальной, если хотя бы один из коэффициентов 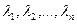не равен нулю.

Определение. Векторы называются линейно зависимыми, если существует их нетривиальная линейная комбинация, равная 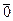. Векторы называются линейно независимыми, если только тривиальная линейная комбинация этих векторов равна нулевому вектору, т.е. из равенства следует, что 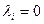для всех .

Теорема.Векторы линейно зависимы тогда и только тогда, когда один из векторов линейно выражается через остальные.

Доказательство. 1). Пусть линейно зависимы. Следовательно, существуют 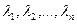, не все равные нулю, такие, что . Предположим, что 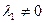. Тогда

 

2). Пусть один из векторов линейно выражается через остальные. Для определенности положим:

.

Тогда . Теорема доказана.

Пример. Рассмотрим пространство Rⁿ – пространство строк длины 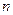. Покажем, что векторы

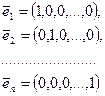
линейно независимы. Действительно, пусть . Но 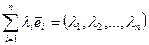, откуда

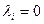для всех , т.е. только тривиальная линейная комбинация векторов 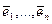равна нулевому вектору.