Метод наименьших квадратов
Сущность метода наименьших квадратов состоит в том, что наивероятнейшими значениями аргументов искомой аналитической зависимости будут такие, при которых сумма квадратов отклонений экспериментальных значений функции  от значений самой функции
от значений самой функции  , будет наименьшей:
, будет наименьшей:  . Обычно функция
. Обычно функция  является функцией нескольких аргументов
является функцией нескольких аргументов  , где
, где  - неизвестные коэффициенты многочлена. Тогда на основании
- неизвестные коэффициенты многочлена. Тогда на основании 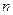 экспериментальных пар
экспериментальных пар  следует определить
следует определить  искомых аргументов аналитической зависимости, которая наилучшим образом описывает массив
искомых аргументов аналитической зависимости, которая наилучшим образом описывает массив  , т.е. в этом случае метод наименьших квадратов требует выполнения условия:
, т.е. в этом случае метод наименьших квадратов требует выполнения условия:
 .
.
Применение метода наименьших квадратов при статистической обработке результатов измерений требует учета ряда условий:
§ Значения аргументов 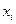 известны точно;
известны точно;
§ Результаты измерений  независимы и содержат лишь случайные погрешности с одинаковыми дисперсиями;
независимы и содержат лишь случайные погрешности с одинаковыми дисперсиями;
§ Погрешности измерения  имеют нормальное распределение.
имеют нормальное распределение.
Первое условие приближенно выполняется за счет измерения значения 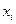 с меньшей погрешностью, чем
с меньшей погрешностью, чем  . Наличие только случайных погрешностей обеспечивается исключением из результатов измерений возможных систематических погрешностей.
. Наличие только случайных погрешностей обеспечивается исключением из результатов измерений возможных систематических погрешностей.
На основе метода наименьших квадратов можно выполнять аппроксимацию различных аналитических зависимостей, например, выражаемых такими полиномами:
 , где a, b, c, d, …, g – константы.
, где a, b, c, d, …, g – константы.
Рассмотрим случай, когда искомая зависимость имеет линейный характер вида  .
.
 При использовании метода наименьших квадратов необходимо по набору из
При использовании метода наименьших квадратов необходимо по набору из 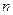 экспериментальных координат (
экспериментальных координат (  ) найти такие оценки неизвестных постоянных a и b, при которых получится прямая линия, наилучшим образом отражающая истинную анализируемую линию.
) найти такие оценки неизвестных постоянных a и b, при которых получится прямая линия, наилучшим образом отражающая истинную анализируемую линию.
График функции – прямая линия с коэффициентом b = tgα, пересекающая ось ординат в точке а.
В соответствии с методом наименьших квадратов наилучшим оценкам a и b соответствуетминимальное значение выражения  , где
, где  - отклонение измеренных значений
- отклонение измеренных значений  от вычисленных при
от вычисленных при  .
.
Эта величина минимальна, если ее частные производные равны нулю:
 и
и  = 0.
= 0.
Решая систему этих двух уравнений, находим формулы для оценок значений a и b:



При этом:
 ;
;  ;
;  ;
;  ;
;  .
.
Степень приближения найденных значений a и b к истинным значениям
Этих величин оценивается с помощью их СКО  и
и  :
:
 ,
,  ,
,
где  - СКО погрешности измерения величины y, значение которой можно получить из паспортных данных на средство измерения или вычислить по формуле:
- СКО погрешности измерения величины y, значение которой можно получить из паспортных данных на средство измерения или вычислить по формуле:
 .
.
В качестве примера практического применения метода наименьших квадратов рассмотрим аппроксимацию нагрузочной характеристики одного из устройств преобразовательной техники. Для построения нагрузочной характеристики измеряют 5 ... 10 пар значений выходного напряжения  и тока нагрузки
и тока нагрузки  . Индекс
. Индекс  соответствует текущему измерению (n – число измерений).
соответствует текущему измерению (n – число измерений).
В данном примере было снято десять пар (n=10) экспериментальных точек  и
и  напряжения и тока соответственно.
напряжения и тока соответственно.
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
 ,B ,B
| 5,35 | 5,20 | 5,11 | 4,92 | 4,76 | 4.76 | 4,50 | 4,33 | 4,30 | 4,04 |
 ,mA ,mA
| 105 | 110 | 129 | 148 | 154 | 181 | 190 | 206 | 225 | 241 |
По полученным экспериментальным результатам построим графическое отображение полученных пар и аппроксимируем их.

Рис. 1 Аппроксимация исследуемой зависимости методом наименьших квадратов
Из расположения экспериментальных точек видно, что аппроксимирующим уравнением может быть полином первой степени типа  . Таким образом, на основании массива экспериментальных данных по уравнениям вычисляем коэффициенты a и b:
. Таким образом, на основании массива экспериментальных данных по уравнениям вычисляем коэффициенты a и b:
 ;
;

Следовательно, исследуемое устройство имеет нагрузочную характеристику, аналитически описываемую как

ПРИМЕР 2
Требуется установить реальную зависимость сопротивления металлического проводника от температуры  по результатам совместных измерений температуры и сопротивления. При этом теоретическая зависимость определена как
по результатам совместных измерений температуры и сопротивления. При этом теоретическая зависимость определена как  , где
, где  - сопротивление проводника при температуре 0 0С;
- сопротивление проводника при температуре 0 0С;  - температурный коэффициент сопротивления проводника;
- температурный коэффициент сопротивления проводника;  - температура в 0С.
- температура в 0С.
 ,0С ,0С
| 10 | 15 | 20 | 25 |
 , Ом , Ом
| 10,3 | 10,9 | 11,3 | 11,6 |
Преобразуем заданную зависимость  в вид
в вид  , где
, где  ,
,  .
.
Расчеты по формулам



 ;
;  ;
;  ;
;  ;
; 
при п=4, 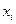 = ti,, и
= ti,, и  дают следующие результаты: а = 9б52 Ом, b = 0,09 Ом/градус.
дают следующие результаты: а = 9б52 Ом, b = 0,09 Ом/градус.
Пусть средство измерения имеет СКО  Ом. Тогда, проведя вычисления по формулам
Ом. Тогда, проведя вычисления по формулам
 ,
,  ,
,
получим:  Ом,
Ом,  Ом/ градус.
Ом/ градус.
Окончательно получаем:

Дата добавления: 2015-10-22; просмотров: 36; Опубликованный материал нарушает авторские права?.