Прямые однократные измерения с точным оцениванием погрешностей

0,95	-	1,1
0,99	>4	1,4
0,99		По графику

Рассмотрим методику точной оценки. Пусть число неисключенных систематических погрешностей равно и каждая задана либо границами , либо доверительными границами , т.е. границами с известной доверительной вероятностью . В первом случае доверительная граница систематической составляющей результата измерения оценивается с задаваемой доверительной вероятностью по формуле , во втором – по формуле , где k – коэффициент, зависящий от значений и , порядок оценки которого приведен в таблице, а - коэффициент, зависящий от и оцениваемый как коэффициент k.

Оценка доверительной границы случайной погрешности результата измерения с задаваемой доверительной вероятностью выполняется в порядке, зависящем от вида представления случайных составляющих (погрешностей средства измерения, метода, оператора).

1. Если случайные составляющие погрешности измерения представлены своими СКО , приведенными в технической документации, то вычисляется по формуле , где - число составляющих; = - аргумент функции Лапласа, приведенной в таблице ранее, соответствующий доверительной вероятности ; - оценка СКО результата однократного измерения величины А. При вероятности принимают = 2, а при - =2,6.

2. Если случайные составляющие погрешности представлены своими СКО , которые были определены на основе эксперимента при числе измерений меньше 20, то вычисляется по формуле , где - коэффициент Стьюдента, определяемый по заданным аргументам по таблице, приведенной ранее. При этом число измерений должно быть равно минимальному числу измерений, которое выполнялось при поиске оценок СКО .

3. Если случайные составляющие погрешности измерений представлены доверительными границами , соответствующими одинаковой доверительной вероятности , тогда значение рассчитывают как

4. Если случайные составляющие заданы доверительными границами с различной доверительной вероятностью , то значение с задаваемой вероятностью находят из выражения , где - оценка СКО результата измерения; и - аргументы функции Лапласа, приведенной в таблице ранее, соответствующие доверительной вероятности ;

 

Суммарная погрешность результата прямого однократного измерения вычисляется в зависимости от соотношения по одной из формул, приведенных в таблице:

 

Значения	Погрешности результата измерения
< 0,8
> 8

 

Значения приведенного в таблице коэффициента К при доверительных вероятностях 0,95 и 0,99 зависят от соотношения и равны:

	0,8
для	0,76	0,74	0,71	0,73	0,76	0,78	0,79	0,81	0,81
для	0,84	0,82	0,80	0,81	0,82	0,83	0,83	0,84	0,85

 

Соответствующим стандартом регламентирована форма записи результата прямого однократного измерения величины :

, где - результат измерения; - доверительная вероятность погрешности результата прямого измерения .

При отсутствии данных о видах функции распределения составляющих погрешности результата прямого однократного измерения или при необходимости дальнейшей обработки результатов, результат измерения представляют в форме , , , .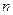