Проверка гипотезы о нормальном распределении результатов наблюдений по составному критерию.

Критерий 1. По результатам наблюдений 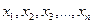вычисляют значение параметра

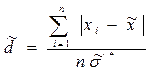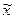, где - результат измерения, 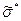- смещенная (относительно математического ожидания) оценка СКО наблюдений: .

Далее выбирают уровень значимости критерия ошибки 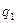, равный 0,02 или 0,1.

По таблице квантилей распределения, зная число наблюдений. Находят предельные значения параметра , являющиеся квантилями нормального распределения:

, .

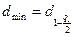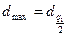Гипотезу о нормальном распределении результатов наблюдений по критерию 1 полагают верной, если .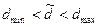

Таблица квантилей распределения

Число наблюдений n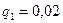
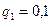
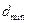
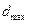
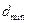
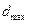
	0,683	0,914	0,724	0,888
	0,695	0,900	0,730	0.877
	0,704	0,890	0,736	0,869
	0,711	0,883	0,740	0,863
	0,717	0,877	0,744	0,858
	0,722	0,872	0,747	0,854
	0,726	0,868	0,750	0,850
	0,730	0,865	0,752	0,848

 

 

Критерий 2.

Для результатов наблюдений 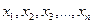вычисляют абсолютную погрешность каждого наблюдения 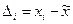и оценку СКО наблюдений 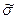по формулам 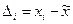и 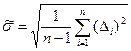. Затем задаются уровнем значимости критерия 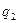, равным 0,01; 0,02 или 0,05. Из таблицы по двум показателям – выбранному 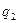и числу наблюдений 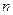находят значение вероятности Р, и только по 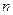- значение теоретического коэффициента .

Значения Р для вычисления

n	m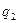
0,01	0,02	0,05
		0,98	0,98	0,96
11…14		0,99	0,98	0,97
15…20		0,99	0,99	0,98
21…22		0,98	0,97	0,96
		0,98	0,98	0,96
24…27		0,98	0,98	0,97
28…32		0,99	0,98	0,97
33…35		0,99	0,98	0,98
36…49		0,99	0,99	0,98

 

Из таблицы ряда значений функции Лапласа 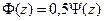, где - интеграл вероятностей, по величине 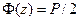находят аргумент функции 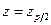и рассчитывают коэффициент .

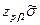И наконец, подсчитывают экспериментальное число 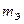модулей погрешностей 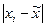, которое должно удовлетворять условию .

 

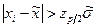Значения функции Лапласа

z
2,0	0,4773	0,4778	0,4783	0,4788	0,4793	0,4798	0,4803	0,4808	0,4812	0,4817
2,1	0,4821	0,4826	0,4830	0,4834	0,4838	0,4842	0,4846	0,4850	0,4854	0,4857
2,2	0,4861	0,4865	0,4868	0,4871	0,4875	0,4878	0,4881	0,4884	0,4887	0,4889
2,3	0,4893	0,4896	0,4898	0,4901	0,4904	0,4906	0,4909	0,4911	0,4913	0,4916
2,4	0,4918	0,4920	0,4922	0,4925	0,4927	0,4929	0,4931	0,4932	0,4934	0,4936
2,4	0,4938	0,4940	0,4941	0,4943	0,4945	0,4946	0,4948	0,4949	0,4951	0,4952
2,6	0,4953	0,4955	0,4956	0,4957	0,4959	0,4960	0,4961	0,4962	0,4963	0,4964
2,7	0,4965	0,4966	0,4967	0,4968	0,4969	0,4970	0,4971	0,4972	0,4973	0,4974
2,8	0,4974	0,4975	0,4976	0,4977	0,4977	0,4978	0,4979	0,4980	0,4980	0,4981
2,9	0,4981	0,4982	0,4983	0,4983	0,4984	0,4984	0,4985	0,4985	0,4986	0,4986

 

Гипотезу о нормальном распределении результатов наблюдения по критерию 2 полагают верной, если 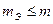. Гипотеза о нормальности распределения принимается, если выполняются оба критерия. Результирующий уровень значимости составного критерия .

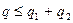Пример: Проверить гипотезу о нормальном законе распределения результатов наблюдения величины х из следующих: 8,619; 8,553; 8, 380; 8,522; 8,498; 8,408; 8,484; 8,283; 8,340; 8,494; 8,526; 8,399; 8,394; 8,561; 8,641; 8,551; 8,420; 8,669 для .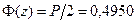

Решение:

Так как число наблюдений лежит в пределах 15...50, то выполняем проверку по составному критерию. Для критерия 1 выбираем уровень значимости . Вычисляем смещенную оценку СКО 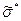и параметр , учитывая погрешности 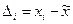каждого наблюдения.

; . Из таблицы квантилей распределения для и находим значения квантилей распределения и , используя при этом линейную интерполяцию величин d. Так как условие 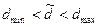выполняется (0,668< 0,834 <0,908), то делаем вывод о нормальности закона распределения результатов наблюдения по критерию 1.

Для критерия 2 задаем уровень значимости критерия . Из таблицы значений Р находим для и значения и . Затем по значению функции Лапласа 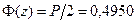из таблицы значений функции Лапласа находим . Используя полученную величину СКО , вычислим коэффициент . Сравнивая величины погрешностей 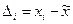с величиной , подсчитываем количество модулей погрешностей 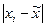, вышедших за 0,277. Таких модулей нет, т.е. 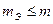.Следовательно, по критерию 2 результаты наблюдений принадлежат к нормальному закону.

Учитывая, что оба критерия выполняются. Гипотеза о нормальности результатов наблюдений величины х принимается с результирующим уровнем значимости составного критерия .