И его среднего квадратического отклонения

при нормальном законе распределения случайной погрешности 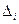за истинную величину 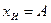принимают ее оптимальную оценку 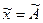, равную оценке математического ожидания 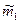выполненного ряда наблюдений , т.е полагают, что 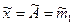есть результат измерения .

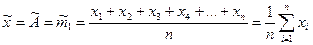Зная 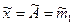истинного значения величины 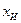, вычисляют абсолютную погрешность каждого из 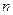наблюдений: .

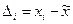Далее найдем оценку СКО наблюдений 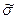, характеризующую точность метода измерений: .

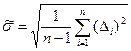Оценка 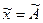измеряемого истинного значения 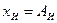зависит от числа наблюдений и является случайной величиной. Поэтому вводят и вычисляют оценку СКО величины 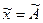, которую называют оценкой среднего квадратического отклонения результата измерения 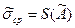. Данное СКО характеризует степень разброса значений 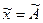по отношению к истинному значению 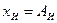и для различных 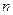определяется как

.

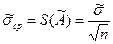Следовательно, точность метода и точность результата многократных наблюдений увеличиваются с ростом числа .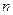

 

Рассмотрим случай многократных наблюдений, когда результат 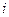-го наблюдения содержит и случайную 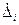и постоянную систематическую 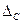погрешности: 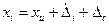. Подстановка значений 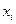в формулу позволяют получить оценку 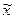результата измерений в виде:

.

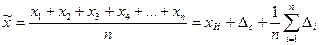Из этого выражения следует, что многократные наблюдения и увеличение их числа не влияют на систематическую составляющую погрешности результатов измерений, но уменьшают случайную (за счет разных знаков реализаций 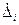). Поэтому в случае, когда в результате многократных наблюдений преобладает систематическая погрешность (например, при использовании прибора низкой точности), целесообразно ограничиться только одним измерением.