Косоугольная фронтальная диметрическая проекция

В косоугольной фронтальной диметрической проекцииось z направлена вертикально вверх, ось х расположена горизонтально, а ось у — под углом 45° к горизонтали (см. табл. 8). Допускается угол наклона оси у под углом 30° и 60°. Коэффициенты искажения по осям х и z равны 1, а по оси у — 0,5.

Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются в окружности без искажения, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, — в эллипсы (рис. 60). Большие оси эллипсов наклонены под углом 7° к осям и равны 1,07 диаметра окружности. Малые оси эллипсов равны 0,33 диаметра окружности.

Линии штриховки параллельны диагоналям квадратов, построенных в плоскостях проекций с учетом коэффициентов искажения (рис. 61).

 

Построение эллипса

Эллипсом называется плоская замкнутая кривая линия, образуемая при пересечении прямого кругового конуса или прямого кругового цилиндра плоскостью, наклонной к их оси и пересекающей все образующие этого конуса или цилиндра.

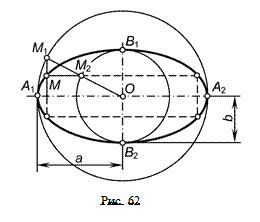
Отрезки прямой, лежащие на осях симметрии эллипса (рис. 62), называются осями эллипса, а концы этих отрезков — вершинами эллипса. Различают большую ось (отрезок А₁А₂) и малую ось (отрезок B₁B₂). Большая и малая оси эллипса взаимно перпендикулярны и в точке пересечения О (центре эллипса) делятся пополам.

Для построения эллипса на двух взаимно перпендикулярных прямых откладываются расстояния, равные большой а и малой b полуосям эллипса. Из центра О проводятся две концентрические окружности радиусами a и b. На большей окружности выбирается произвольная точка М₁, и проводится радиус М₁О, который в пересечении с малой окружностью дает точку М₂. Из точки М₁ проводится прямая, параллельная малой оси эллипса, а из точки М₂ — прямая, параллельная большой оси эллипса. При пересечении этих прямых образуется точка М, принадлежащая эллипсу. Построив одну точку эллипса, можно построить еще три точки, расположенные симметрично относительно осей эллипса и его центра.

Далее в том же порядке можно построить ряд точек, принадлежащих эллипсу. Искомый эллипс образуется при соединении плавной кривой линии с помощью лекала построенных точек, а также точек А₁, А₂, B₁и B₂, являющихся вершинами эллипса.