ВЫПОЛНЕНИЕ ЧЕРТЕЖА ДЕТАЛИ С СОПРЯЖЕНИЯМИ
Цель работы: изучить выполнение сопряжений кривых, выполнить чертеж детали с сопряжениями
1. Деление окружностей на равные части
Деление окружности 4 и 8 равных частей
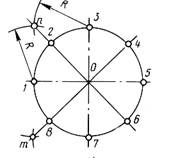
1) Два взаимных перпендикуляра диаметра окружности делят ее на 4 равные части (точки 1, 3, 5, 7).
2) Далее делят прямой угол на 2 равные части (точки 2, 4, 6, 8) (рисунок 1 а).
Деление окружности на 3, 6, 12 равных частей
1) Для нахождение точек, делящих окружность радиуса R на 3 равные части, достаточно из любой точки окружности, например точки А(1), провести дугу радиусом R.(т.2,3) (рисунок 1 б).
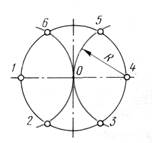
2) Описываем дуги R из точек 1 и 4 (рисунок 1 в).
3) Описываем дуги 4 раза из точек 1, 4, 7, 10 (рисунок 1 г).

а б в


г д е
Рисунок 1 – Деление окружностей на равные части
а – на 8 частей; б – на 3 части; в – на 6 частей;
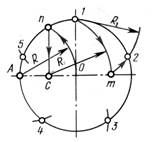
г – на 12 частей; д – на 5 частей; е – на 7 частей.
Деление окружности на 5, 7, равных частей
1) Из точки А радиусом R проводят дугу, которая пересекает окружность в точке n. Из точки n опускают перпендикуляр на горизонтальную осевую линию, получают точку С. Из точки С радиусом R1=С1, проводят дугу, которая пересекает горизонтальную осевую линию в точке m. Из точки 1 радиусом R2=1m, проводят дугу, пересекающую окружность в точке 2. Дуга 12=1/5 длины окружности. Точки 3,4,5 находят, откладывая циркулем отрезки, равные m1 (рисунок 1 д).
2) Из точки А проводим вспомогательную дугу радиусом R, которая пересекает окружность в точке n. Из нее опускаем перпендикуляр на горизонтальную осевую линию. Из точки 1 радиусом R=nc, делают по окружности 7 засечек и получают 7 искомых точек (рисунок 1 е).
2. Построение сопряжений
Сопряжением называется плавный переход одной линии в другую.
Для точного и правильного выполнения чертежей необходимо уметь выполнять построения сопряжений, которые основаны на двух положениях:
1. Для сопряжения прямой линии и дуги необходимо, чтобы центр окружности, которой принадлежит дуга, лежал на перпендикуляре к прямой, восстановленном из точки сопряжения (рисунок 2 а).
2. Для сопряжения двух дуг необходимо, чтобы центры окружностей, которым принадлежат дуги, лежали на прямой, проходящей через точку сопряжения (рисунок 2 б).

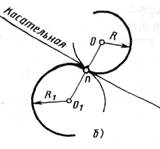
Рисунок 2 – Положения о сопряжениях
а – для прямой и дуги; б – для двух дуг.
Сопряжение двух сторон угла дугой окружности и заданного радиуса
Сопряжение двух сторон угла (острого или тупого) дугой заданного радиуса выполняют следующим образом:
Параллельно сторонам угла на расстоянии, равном радиусу дуги R, проводят две вспомогательные прямые линии (рисунок 3 а, б). Точка пересечения этих прямых (точка О) будет центром дуги радиуса R, т.е. центром сопряжения. Из центра О описывают дугу, плавно переходящую в прямые — стороны угла. Дугу заканчивают в точках сопряжения n и n1, которые являются основаниями перпендикуляров, опущенных из центра О на стороны угла. При построении сопряжения сторон прямого угла центр дуги сопряжения проще находить с помощью циркуля (рисунок 3 в). Из вершины угла А проводят дугу радиусом R, равным радиусу сопряжения. На сторонах угла получают точки сопряжения n и n1. Из этих точек, как из центров, проводят дуги радиусом R до взаимного пересечения в точке О, являющейся центром сопряжения. Из центра О описывают дугу сопряжения.
|
|
|
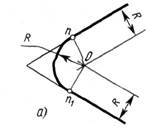


Рисунок 3 – Сопряжения углов
а – острого; б – тупого; в – прямого.
Сопряжение прямой с дугой окружности
Сопряжение прямой с дугой окружности может быть выполнено с помощью дуги с внутренним касанием (рисунок 4 б) и дуги с внешним касанием (рисунок 4 а).
Для построения сопряжения внешним касанием проводят окружность радиуса R и прямую АВ. Параллельно заданной прямой на расстоянии, равном радиусу r (радиус сопрягающей дуги), проводят прямую ab. Из центра О проводят дугу окружности радиусом, равным сумме радиусов R и r, до пересечения ее с прямой ab в точке О1. Точка О1 является центром дуги сопряжения.
Точку сопряжения с находят на пересечении прямой ОО1 с дугой окружности радиуса R. Точка сопряжения С1 является основанием перпендикуляра, опущенного из центра О1 на данную прямую АВ. С помощью аналогичных построений могут быть найдены точки О2, С2, С3.
На рисунке 6 б выполнено сопряжение дуги радиуса R с прямой АВ дугой радиуса r с внутренним касанием. Центр дуги сопряжения О1 находится на пересечении вспомогательной прямой, проведенной параллельно данной прямой на расстоянии r, с дугой вспомогательной окружности, описанной из центра О радиусом, равным разности R-r. Точка сопряжения является основанием перпендикуляра, опущенного из точки О1 на данную прямую. Точку сопряжения с находят на пересечении прямой ОО1 с сопрягаемой дугой.
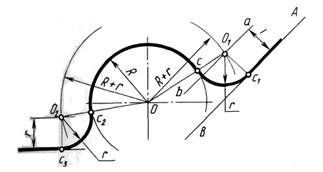

а б
Рисунок 4 – Сопряжение дуги с прямой
а – с внешним касанием; б – с внутренним касанием.
Сопряжение дуги с дугой
Сопряжение двух дуг окружностей может быть внутренним, внешним и смешанным.
При внутреннем сопряжении центры О и О1 сопрягаемых дуг находятся внутри сопрягающей дуги радиуса R (рисунок 5 а).
При внешнем сопряжении сопрягаемых дуг радиусов R1 и R2 находятся вне сопрягающей дуги радиуса R (рисунок 5 б).
При смешанном сопряжении центр О1 одной из сопрягаемых дуг лежит внутри сопрягающей дуги радиуса R, а центр О другой сопрягаемой дуги вне ее (рисунок 5 в).



а б в
Рисунок 5 – Сопряжения дуг
а – внутреннее; б – внешнее; в – смешанное.
При вычерчивании контуров сложных деталей важно уметь распознавать в плавных переходах те или иные виды сопряжений и уметь их вычерчивать.
Для приобретения навыков в построении сопряжений выполняют упражнения по вычерчиванию контуров сложных деталей. Для этого необходимо определить порядок построения сопряжений и только после этого приступать к их выполнению.
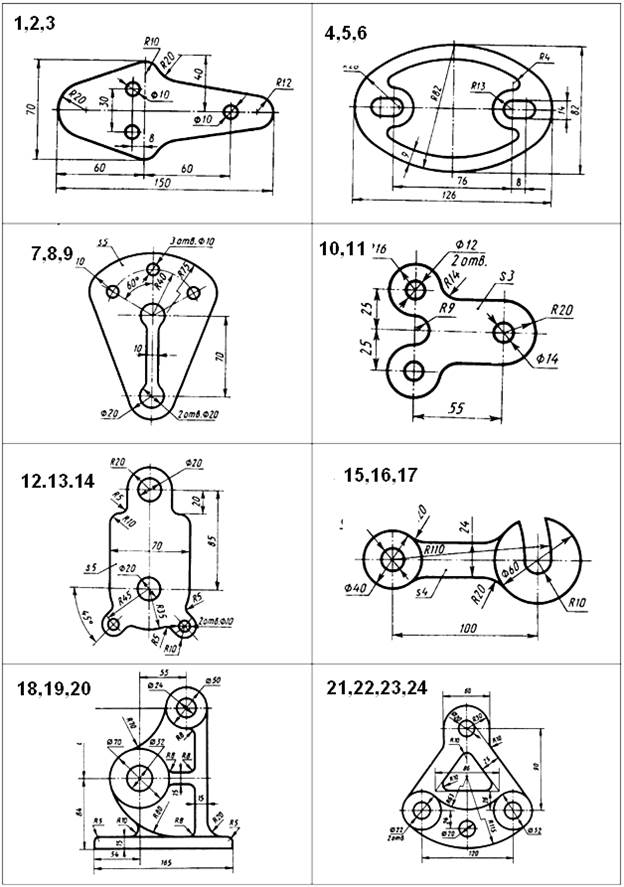
ЗАДАНИЕ: Вычертить изображения контуров деталей, указанных на рисунке задания, нанести размеры. Задание выполнить на листе чертежной бумаги формата А4.
Указания по выполнению задания
При выполнении каждой задачи должна соблюдаться определенная последовательность геометрических построений:
– осевые, центровые линии, основные начертательные;
– дуги, закругления;
– обводка, штриховка, выносные линии;
– размеры.
Варианты задания