Указания к выполнению работы

Перспективные проекции в архитектурной практике используются для оценки эстетических достоинств объекта на стадии проектирования. Перспективой называется изображение, полученное методом центрального проецирования на картинную плоскость.

Перспективные проекции зданий или сооружений строятся по их ортогональным проекциям. Существует несколько способов построения перспектив, в данной работе используется метод архитекторов. Этот способ сводится к определению проекций точек сооружения на картинную плоскость лучами, идущими из точки зрения к каждой точке сооружения.

1. На листе бумаги выполнить ортогональные проекции здания, согласно номеру варианта, при этом увеличив изображение не менее чем в 2 раза.

2. Ортогональные проекции на листе разместить в левом верхнем углу, если след картины проведен через правый угол здания и в правом верхнем, если след картины проведен через левый угол здания (рис.1.2.20)

Рис.1.2.20

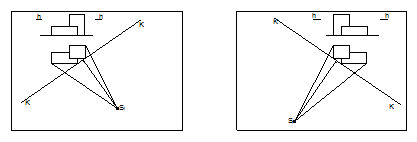
На горизонтальной проекции здания нанести предварительно заданное положение следа картины К, на фронтальной проекции отметить положение линии горизонта h.

 

3. Точка зрения на ортогональном чертеже определяется точкой стояния S₁ (горизонтальная проекция точки зрения S) и высотой линии горизонта. Для построения малоискаженного перспективного изображения объекта при выборе точки зрения необходимо учесть следующее: точка стояния должна находиться от основания картины на таком расстоянии, чтобы горизонтальная проекция

4. угла зрения (угол между проецирующими лучами, проведенными в крайнюю левую и правую точки плана здания) составляла 28-35⁰. Положение точки стояния выбрать так, чтобы на перспективе были видны выступающие и углубляющиеся части здания. Высота точки зрения определяется положением линии горизонта и принимается чаще всего от 1,7 до 2,0 м, что соответствует высоте уровня глаз человека. При значительной высоте здания или сооружения следует проверить угол зрения в вертикальной плоскости, половина этого угла не должна превышать 30⁰. Угол наклона картины к фасадной плоскости объекта принимается в пределах 25…30⁰.

Через построенную на плане точку стояния S₁ провести горизонтальные проекции лучей зрения к крайним левому и правому углам здания. Из точки S₁ провести перпендикуляр к основанию картины S₁P₀. Точка P₀ должна находиться в пределах средней трети расстояния между проекциями крайних углов здания на картинную плоскость. Если это необходимо корректируем расположение картинной плоскости.

5. Чтобы определить проекции точек схода F_1к и F_2к необходимо выбрать два основных (доминирующих) направления плана здания. Параллельно этим направлениям проводим лучи из точки S₁ до пересечения с основанием картины. Точки пересечения с основанием картиной плоскости (картины) будут искомыми точками F_1к и F_2к. Точки F₁ и F₂ будут находиться на линии горизонта (рис1.2.21).

Рис.1.2.21

 

 

6. Из вершин плана здания проводим лучи в точку S₁. Пересекая линию основания картинной плоскости лучи фиксируют перспективное изображение вершин объекта (1₀, 2₀, 3₀, …, N₀) (рис.1.2.22).

7. Ввиду того, что перспективные проекции здания получаются уменьшенными по отношению к размерам на ортогональном чертеже, все размеры в перспективе лучше пропорционально увеличить в 2..3 раза: высоту горизонта, расстояния по картине, истинные величины вертикальных прямых.

При построении перспективы на поле чертежа выбрать положение главной точки Р (примерно на середине формата, если линия горизонта проходит на уровне 1,7-2м, и в верхней части середины формата, если линия горизонта проходит выше здания) и провести через нее линию горизонта h-h. Ниже линии горизонта на расстоянии, равном высоте точки зрения, провести основание картины к-к.

8. На линию основания картины к-к с плана (с помощью размеченной полоски бумаги) переносят точки 1₀, 2₀, 3₀, …, N₀ а также F_1к и F_2к, совместив при этом положение точки Р. Если положение точек схода F₁ и F₂ определяется за пределами формата, можно подклеить полоски бумаги (рис.1.2.23).

9. Из точек F_1к и F_2к проводят перпендикуляры до пересечения с линией горизонта h-h. Получим точки схода F₁ и F₂.

 

Рис.1.2.22 рис.1.2.23

 

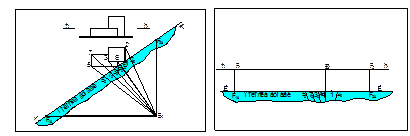
10. Построение перспективы следует начинать с видимой части стен здания. Из точки 1, лежащей на основании картины, провести прямые в точки схода F₁ и F₂, а также вертикальную прямую (угол здания). Величина вертикальной прямой или высота точки в перспективе будут натуральными, если прямая или точка расположены в картинной плоскости. В данном случае картина проведена через угол здания 1. Следовательно угол 1 спроецируется в истинную величину. Замеряем высоту стены (угла) в ортогональных проекциях Н1 и откладываем по вертикальной прямой от основания картины. Полученную верхнюю точку также соединяем с точками F₁ и F₂. Из точек 2₀ и 3₀ проводим вертикальные прямые, которые ограничат стены здания (рис.1.2.24).

В данном примере угол 4 также находится на картинной плоскости, поэтому из т.4 проводим перпендикуляр, на

 

Рис.1.2.24

 

котором от основания картины откладываем натуральную

высоту данной части здания Н2. Полученную верхнюю точку также соединяем с точками F₁ и F₂. Из точки 5₀ проводим вертикальную линию, которая ограничит стену (рис1.2.25).

 

Рис.1.2.25

 

Точка пересечения линий 1F₁ и 4F₂ должна лежать на перпендикуляре из точки 6₀. Это линия пересечения двух объемов здания (двух параллелепипедов). Из полученной точки пересечения перпендикуляра с верхней гранью стены проводим луч на точку схода F₁ и определяем точку пересечения с перпендикуляром в точке 3₀ (рис.1.2.26).

 

Рис.1.2.26

 

 

Выделяем видимые линии среди линий построения и перспектива объекта примет следующий вид ( рис.1.2.27 ).

 

Р1.2.27

 

11. Если вертикальная прямая или точка расположены не в картинной плоскости, то истинная величина определяется путем <<выноса>> их на картинную плоскость по прямым параллельным одному из доминирующих направлений линий здания (рис.1.2.28).

 

Рис.1.2.28

1)

 

2) 3) 4)

 

12. Построение собственных и падающих теней.

Построение тени в перспективе начинают с выбора источника света. Его можно выбрать произвольно, но при этом, следует помнить, что от выбора освещения, зависят наглядность и реалистичность изображения. Целесообразно лучи света расположить параллельно картинной плоскости, тогда они изобразятся и на перспективе параллельными, а их вторичные проекции – параллельными основанию картины, т.е. горизонтальными. Угол наклона светового луча принимают в пределах от 30 до 60⁰.

Согласно выбранному направлению освещения, определяются собственные тени. Неосвещенные поверхности здания будут отбрасывать падающие тени (рис.1.2.29).

 

 

Рис.1.2.29

 

 

 

 

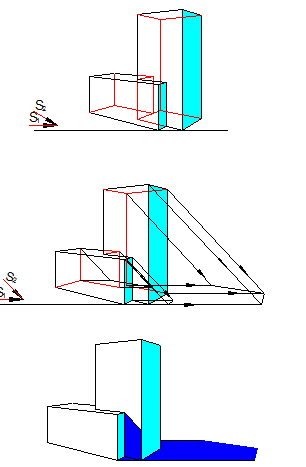
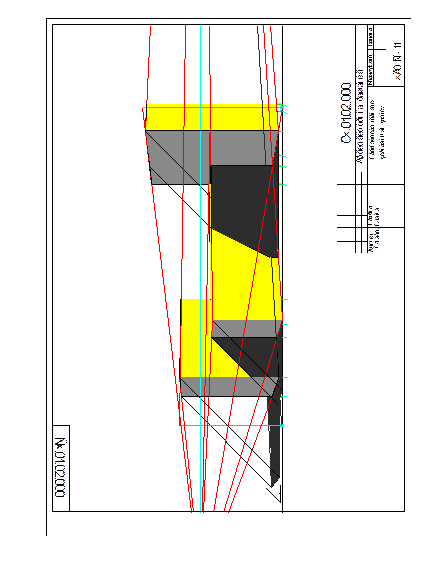
рис.1.2.30 Пример выполнения работы

 

 

Рис.1.2.31 Аппарат построения перспективы

return false">ссылка скрыта

 

 

3 Метод проекций с числовыми отметками

 

 

Метод проекций с числовыми отметками имеет широкое применение в проектировании различных инженерных земляных сооружений, когда высота объекта существенно меньше его размеров в плане (строительная площадка, насыпь, дамба, плотина, дорога и др.).

Этот метод выполняется на основе прямоугольного проецирования геометрических объектов только на горизонтальную плоскость, которая называется плоскостью нулевого уровня. Рядом с обозначением проекции указывается её удаление от плоскости нулевого уровня (т.е. координата Z). Это число называется числовой отметкой. Перед числовой отметкой ставится знак (-), если точка расположена ниже плоскости нулевого уровня, если выше плоскости – положительные отметки (рис.1.3.1).

Рис.1.3.1

 

Чертежи проекций с числовыми отметками называются планами. На данных чертежах всегда указывается линейный масштаб с обозначением единицы измерения (м, см). Им пользуются при решении задач.

 

Чертёж прямой. Градуирование прямой.

 

Прямая считается заданной, если на плоскость П₀ предоставлены проекции 2х её точек. Проекция прямой А(4)В(-2) на плоскость П₀ называется заложением прямой l_АВ .

Рис.1.3.2

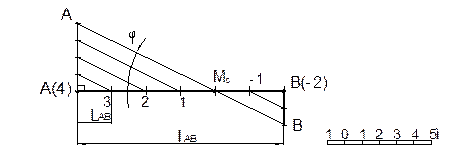
Проградуировать прямую, значит определить на ней проекции точек с целыми значениями отметок, отличающиеся друг от друга на единицу. Заложение прямой, соответствующее единице превышения, называется интервалом L_АВ (рис.1.3.2).

Чтобы найти натуральную величину прямой нужно в точках прямой провести перпендикуляры равные превышению данной точки в масштабе.

Уклон прямой – это отношение разности превышения точек прямой к её заложению.

 

Взаимное положение прямых

 

1 Пересекающиеся прямые

У пересекающихся прямых проекции пересекаются, а точки на прямых в месте пересечения проекций имеют одинаковую отметку.

Для оценки взаимного расположения прямых их нужно проградуировать (рис.1.3.3).

 

Рис.1.3.3

 

2 Параллельные прямые

Если прямые параллельны в пространстве, то параллельны их горизонтальные проекции, равны углы наклона к плоскости проекций и числовые отметки возрастают в одном направлении, интервалы равны (рис.1.3.4).

Рис.1.3.4

3 Скрещивающиеся прямые

У таких прямых точки в месте пересечения имеют разные отметки. Для оценки взаимного положения прямые градуируют (рис.1.3.5).

Ри1.3.5

 

 

Плоскость

 

Введём некоторые понятия. В проекциях с числовыми отметками плоскость можно задать масштабом уклона плоскости – это проградуированная проекция линии наибольшего наклона плоскости ( линия наибольшего ската перпендикулярна к горизонталям плоскости). Масштаб уклона плоскости задается двойной линией – толстой и тонкой обозначается α_ί (рис.1.3.6). Рис.1.3.6

 

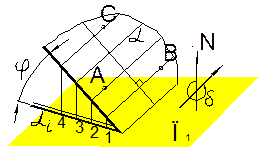
Направление простирания – это правое направление горизонталей плоскости α, если смотреть в сторону возрастания отметок пот линии наибольшего ската плоскости.

Угол простирания (δ) – угол , образованный между северным направлением магнитной стрелки и направлением простирания, измеренный против часовой стрелки.

Угол падения (γ) наклона – угол наклона между линией наибоением простирания, измеренный против часовой стрелки.

Угол падения (γ) наклона – угол наклона между линией наибольшего ската и масштабом уклона α_ί этой плоскости.

Проградуировать плоскость, заданную А₅В₇С₂, т.е. построить горизонтали плоскости с целыми значениями отметок. Для этого проградуируем сторону ВС, имеющую наибольшую разность отметок. Соединим точку А5 с 5ой отметкой на стороне ВС. Эта линия – проекция горизонтали плоскости. Линия перпендикулярная проекциям горизонталей – масштаб уклона плоскости. Затем определяем направление простирания и угол простирания плоскости (рис.1.3.7).

Рис.1.3.7

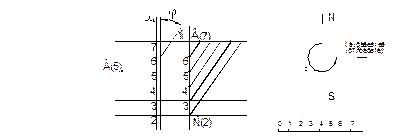
Задача: Определить линию пересечения двух плоскостей, заданных масштабами уклонов Ρ_ί и Σ_ί..

Линия пересечения плоскостей пройдет через точки пересечения горизонталей, имеющие одинаковые отметки. В точке К7 пересекаются горизонтали плоскостей, имеющие отметку (7), а в точке М2 – имеющие отметку (2). Прямая К7М2 – искомая линия пересечения плоскостей Ρ и Σ (рис.1.3.8).

Рис.1.3.8

Задача: Определитьлинию пересечения плоскости Σ, заданной масштабом уклона Σ_ί с топографической поверхностью, заданной совокупностью расположенных на ней кривых линий – горизонталей.

Задача решается аналогично. Определяются точки пересечения горизонталей с одинаковыми числовыми отметками (рис.1.3.9).

Топографической называют поверхность, образование которой не подчиняется какому-либо геометрическому закону. К таким поверхностям относят : поверхность земной коры, корпус судна, самолёта и т.д..

Рис1.3.9

 

 

 

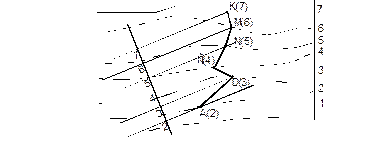
Работа №3