Указания к выполнению работы

Тени здания

Цель работы: изучить метод построения теней здания в ортогональных проекциях.

Содержание работы: Построить падающие тени здания в ортогональных проекциях. Индивидуальное задание взять из приложения 1.

Оформление работы: чертеж выполнить карандашом на чертежной бумаге формата А3. Фасад и тени отмыть акварельными красками. Линии построения сохранить. Пример выполнения работы смотри рисунок 1.1.14.

Порядок выполнения работы

1. Ознакомится с содержанием индивидуального задания.

2. Вычертить ортогональные проекции (план и фасад) здания.

3. Показать направление лучей.

4. Построить тени в ортогональных проекциях.

5. Выполнить отмывку.

6. Обвести чертеж. Линии построения сохранить.

7. Защитить работу.

 

Указания к выполнению работы

Согласно номеру варианта выбрать номер рисунка из приложения.

Ортогональные проекции выполнить на листе чертежной бумаги формата А3, увеличив при этом изображение не менее чем в 2 раза. План под фасадом расположить так, чтобы расстояние между ними было не менее полной высоты здания.

Тень от объекта, состоящего из нескольких геометрических тел, определяется как совокупность теней от простых геометрических объемов. В данном задании от 4х параллелепипедов.

На основании рассмотренных ранее примеров видно:

что падающая тень параллельна самой фигуре, если данная фигура параллельна плоскости, на которую падает от нее тень;

падающая тень отрезка перпендикулярного плоскости, есть отрезок, совпадающий с направлением проекции луча независимо от того, на какую поверхность эта тень падает;

падающая тень равна и параллельна тени от двух равных и параллельных между собой отрезков;

падающая тень фигуры, лежащей в лучевой плоскости, т.е. параллельно лучам света, будет отрезком прямой линии;

падающая тень от какого-либо выступа, перпендикулярного вертикальной плоскости, по ширине равна этому выступу.

Таким образом, чтобы найти тени на фасаде здания, необходимо вначале внимательно прочитать чертеж, затем проанализировать каждый выступ, каждую линию, после чего приступить к построению теней. Построение теней производится постепенно. Последовательно строятся тени от многогранников (рис.1.1.12). Затем определяется контур падающей тени от всего объекта и определяются тени от выступающих частей здания (рис.1.1.13).

 

 

Рис.1.1.12

 

Рис.1.1.13

 

 

Рис.1.1.14

 

Приложение 1

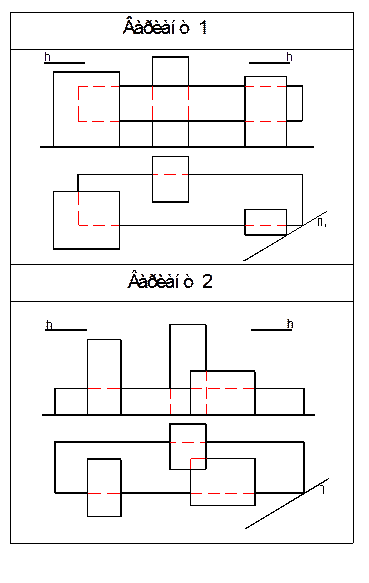
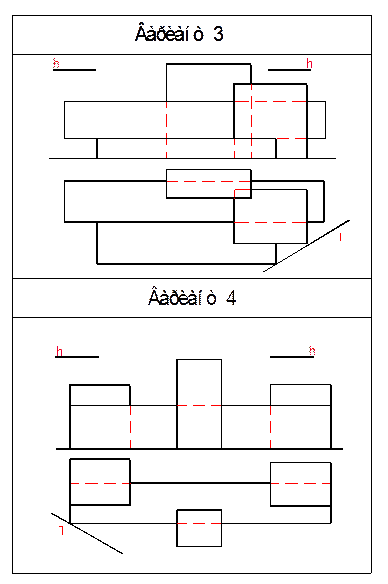
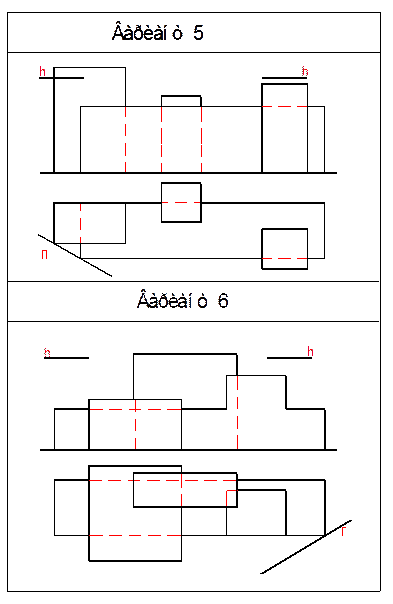
2 Перспективные проекции

 

 

Перспективной проекцией (перспективой) называется центральная проекция объекта на плоскость (поверхность). Перспектива – латинское слово означает смотреть сквозь.

Перспектива является одним из методов построения наглядных изображений. В зависимости от поверхности, на которой строятся перспективные проекции, различают следующие виды перспективы:

1 Линейная перспектива – проецирование на вертикальную плоскость.

2 Плафонная перспектива – проецирование на горизонтальную плоскость.

3 Панорамная перспектива – проецирование на цилиндрическую плоскость.

4 Купольная перспектива – проецирование на сферу.

Определим основные понятия для линейной перспективы (рис.1.2.1).

Горизонтальная плоскость проекций, на которой располагается объект проецирования, называется предметной плоскостью и обозначается П₁.

Перпендикулярная ей плоскость, на которую осуществляется перспективное проецирование, называется картинной плоскостью или картиной и обозначается К.

Центр проецирования называется точкой зрения и обозначается S.

Пространство между точкой зрения S и картиной является промежуточным пространством.

Пространство за картинной плоскостью называется предметным пространством.

Мнимое пространство расположено за точкой зрения S в направлении обратном главному лучу SP.

Горизонтальная плоскость, проходящая через точку зрения S, называется плоскостью горизонта, а линия пересечения ее с картинной плоскостью называется линией горизонта и обозначается h-h.

Линия пересечения картинной и предметной плоскостей называется основанием картины и обозначается К-К.

Перпендикуляр, опущенный из точки зрения S, на картинную плоскость называется главным лучом, а точка его пересечения с картинной плоскостью называется главной точкой картины и обозначается Р. Горизонтальные проекции точек (проекции на предметную плоскость) называются основаниями точек.

Рис.1.2.1

 

П ₁ - предметная плоскость

К – картинная плоскость

КК – основание картины

hh – линия горизонта

S – точка зрения

S₁ – точка стояния

Р – главная точка картины

Р_{1 –} основание главной точки

SP – главный луч

 

 

Перспектива точки

 

Для построения перспективы точки необходимо провести луч от зрителя (точка зрения) в точку А. Точка пересечения луча с картинной плоскостью А_к является перспективным изображением точки А.

При рассмотрении центрального проецирования было установлено, что одна проекция точки не определяет ее положения в пространстве. Поэтому на картинной плоскости строят не только перспективную проекцию точки А_к, но и ее вторичную проекцию А_1к (это перспектива основания точки А). Для определения вторичной проекции необходимо провести луч от точи зрения S к основанию точки А₁ (проекция точки А на плоскость П₁). Точка пересечения данного луча с картинной плоскостью и будет вторичной проекцией точки А А_1к (рис.1.2.2).

 

Рис.1.2.2

 

Рассмотрим точку А в предметном пространстве. Последим за изменением перспективы и вторичной проекции точки А при ее удалении вдоль проецирующего луча SA. ЕЕ перспектива остается по прежнему в точке А_к, а вторичная проекция смещается вертикально вверх, т.е. по мере удаления вторичная проекция будет приближаться к линии горизонта (рис.1.2.3). Тогда, вторичная проекция бесконечно удаленной точки, будет находиться на линии горизонта .

 

 

рис.1.2.3

Чем ближе точка к картине, тем меньше расстояние от ее вторичной проекции до основания картины.

Вторичные проекции точек находящихся в промежуточном пространстве, будут определяться ниже основания картины.

Вторичные проекции точек, расположенных в мнимом пространстве, будут определяться выше линии горизонта.

Если точка лежит в картинной плоскости, то ее вторичная проекция будет находиться на основании картины.

Таким образом, по вторичной проекции можно установить, в каком пространстве находится точка.

 

Перспектива прямой

Прямая на чертеже определяется перспективой двух точек, и может занимать различные положения. Перспективное изображение прямой обратимо, если оно дополнено вторичной проекцией. Задание только одной перспективы прямой не определяет ее положения в пространстве.

На рис.1.2.4 перспектива прямой и ее вторичная проекции определены перспективами и вторичными проекциями двух ее точек А и В.

Проецирующие лучи, которые проходят через точку S и некоторую прямую АВ, образуют плоскость. Эта лучевая плоскость пересекает картину по прямой А^/ В^/, представляющей собой перспективу заданной прямой.

return false">ссылка скрыта

Рис.1.2.4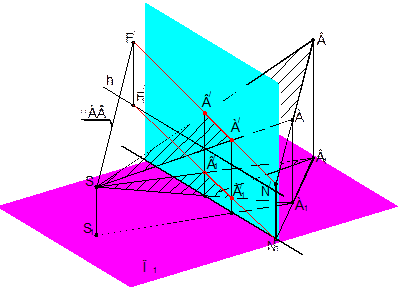

 

 

Имея А^/В^/ и А₁^/В₁^/, можно определить две характерные точки прямой: перспективу F^/ бесконечно удаленной (несобственной ) точки F и начало прямой N^/ (началом прямой принято называть точку пересечения прямой с картиной). Вторичная проекция первой из них ( точка F₁^/) должна быть на линии горизонта, а второй на основании картины ( точка N₁^/). Проведя через F₁^/ вертикальную прямую до пересечения А^/В^/, получим перспективу F^/ бесконечно удаленной точки прямой. В этой точке с картиной пресечется проецирующий луч, направленный в бесконечно удаленную точку данной прямой АВ (параллельный АВ). Перпендикуляр к основанию К-К картины, проходящий через N^/₁, пересекаясь с А^/В^/, определяет начало прямой (точку N^/).

 

 

Рис.1.2.5

 

Положение перспективы несобственной точки прямой на картине позволяет судить о том, как прямая расположена в пространстве. Если точка F^/ оказалась над линией горизонта (рис.1,2.5), то прямая АВ – восходящая, так как луч, проведенный из точки зрения параллельно данной прямой , направлен кверху. Если точка F^/ находится под линией горизонта, то прямая АВ – нисходящая (рис.1.2.6). Если перспектива несобственной точки лежит на линии горизонта, то прямая АВ расположена горизонтально (рис1.2.7 ).

 

Рис.1.2.6 Рис.1.2.7

 

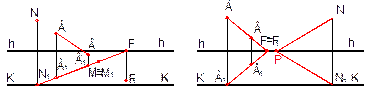
Если прямая перпендикулярна плоскости картины, то её несобственная точка определяется лучом, проведенным из точки зрения перпендикулярно плоскости картины, и совпадет с главной точкой картины Р.

Если прямая перпендикулярна предметной плоскости, её вторичная проекция становится точкой.

 

Методы построения перспективы.

 

1. Радиальный метод. Сущность этого методазаключается в определении точекпересечения лучей с картинной плоскостью, поэтому его часто называют методом следа луча.

Радиальный метод не требует знания теории перспективы. Предмет, точка зрения и картинная плоскость изображаются на эпюре. На этом же эпюре создаются проекции проецирующих лучей и определяются точки пересечения их с картиной. Радиальный метод оказывается рациональным при построении перспективы предмета, в плане которого много не параллельных между собой линий.

Метод масштабов.

3 Метод архитекторов. В основу метода положено свойство перспективных проекций параллельных прямых, которое заключается в том, что они сходятся в одной точке – точке схода F. Этот способ применяется при построении перспективных изображений различных сооружений, имеющих в плане два доминирующих направления линий. В качестве картины выбрана горизонтально проецирующая плоскость, которую целесообразно провести через один из углов предмета. Положение точки зрения S определяется углом зрения, ограниченным лучами в крайние точки плана.

 

Построение перспективы геометрических тел методом архитекторов.

 

Рассмотрим построение перспективы двух параллелепипедов, расположенных на одном уровне (рис.1.2.8). Картинную плоскость проводим через угол 1, а линию горизонта проведём так , чтобы у параллелепипеда 1234 было видно верхнее основание, а у параллелепипеда АВСD верхнее основание будет невидимым.

 

Рис.1.2.8

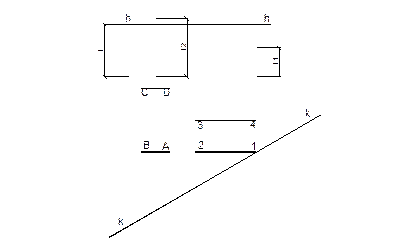
Точку зрения располагаем так, чтобы главный луч зрения был перпендикулярен картинной плоскости (картине) и главная точка Р располагалась в средней трети картины.

Через все точки фигур проводим лучи в точку зрения. Затем находим левую и правую точки схода F₁ и F₂. Для этого определяем два доминирующих направления сторон параллелепипедов и параллельно этим направлениям проводим лучи из точки зрения до пересечения с картинной плоскостью (рис.1.2.9).

Рис1..2.9

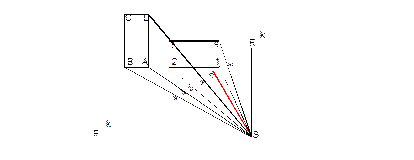
Затем след картинной плоскости вместе со всеми точками переносим на то место, где будет строиться перспективное изображение (рис.1.2.10).

Рис.1.2.10

 

На расстоянии Н от основания картины к-к проводим параллельную линию h-h, которая является линией горизонта. Точки схода F₁ и F₂ переносим на линию горизонта (рис.1.2.11).

Рис.1.2.11

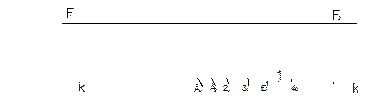
Из т.1 на основании картины проводим перпендикуляр и откладываем высоту Н1, затем из конечных точек отрезка проводим лучи на точки схода F₁ и F₂, а проведя перпендикуляры из точек 2₀ и 4₀ ограничим грани параллелепипеда (рис.1.2.12).

Рис.1.2.12

 

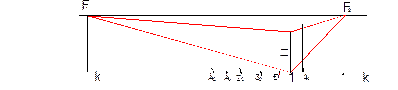
Чтобы построить видимую верхнюю поверхность, нужно из точек пересечения лучей, проведенных от перпендикуляра в т.1, и перпендикуляров в т.т. 2₀ и 4₀, провести лучи на точки схода (рис.1.2.13).

Рис.1.2.13

 

 

Таким образом получаем перспективу параллелепипеда 1234 (рис.1.2.14).

Рис.1.2.14

 

 

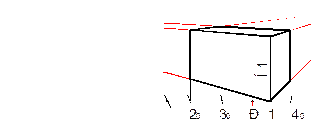
Параллелепипед АВСD расположен на расстоянии от картинной плоскости, для того чтобы отложить истинную высоту данного объекта, необходимо <<вынести>> одну из сторон на картинную плоскость. Продолжим сторону AD до пересечения с картинной плоскостью (рис.1.2.15 ), затем перенесем полученную точку А_к на основание картины , где выполняется построение перспективы. Из т.А_к проводим перпендикуляр к основанию картины и откладываем истинную высоту Н2. Затем соединим конечные точки полученного отрезка с точками схода F₁ и F₂ (рис.1.2.16 ).

 

 

Рис.1.2.15 рис.1.2.16

Проведя перпендикуляры из точек А₀ и D₀ мы определим размеры стороны АD в перспективе (рис1.2.17 ). Затем достраиваем сторону АВ (рис.1.2.18).

 

Рис1..2.17 рис.1.2.18

В результате построений получаем перспективу двух геометрических тел (рис.1.2.19).

Рис.1.2.19

 

Работа № 3

 

Перспектива здания

Цель работы: Изучить метод архитекторов для построения перспективы здания, построения теней в перспективе.

Содержание работы: По заданным ортогональным проекциям здания, линии горизонта и положению картинной плоскости построить его перспективу. Построить собственные и падающие тени.

Оформление работы: чертеж выполнить карандашом наwidth:580px;height:400px" data-ad-client="ca-pub-1201569435861782" data-ad-slot="9319239531">