Способы преобразования чертежа.

Метод плоскопараллельного перемещения.

В зависимости от положения этих плоскостей по отношению к плоскостям проекций и вида траектории метод плоскопараллельного перемещения подразделяют на способы:

а) способ параллельного перемещения.

Плоскопараллельным перемещением геометрической фигуры в пространстве называется такое ее перемещение, при котором все точки фигуры перемещаются в параллельных друг другу плоскостях. При этом строятся новые проекции фигуры в частном положении по отношению к прежним плоскостям проекции.

Рассмотрим плоскопараллельное перемещение на примере рис. 5.15 — преобразования прямой общего положения в прямую уровня — фронталь. Выполним плоскопараллельное движение прямой АВ относительно горизонтальной плоскости проекций П₁. Точки А и В перемещаются в горизонтальных плоскостях. Суть построений заключается в том, что мы перемещаем проекцию А₁В₁ так, чтобы она стала параллельна оси П₁/П₂ и затем достраиваем проекцию A₂'B₂' на П₂. Таким образом мы получаем ту же прямую, но перемещенную в новое состояние параллельное П₂.

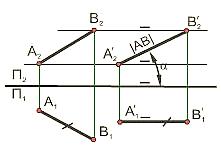Алгоритм графических построений:

1) Из произвольной точки A₁' параллельно оси П₁/П₂ откладываем расстояние равное длине проекции А₁В₁;

2) Проводим линии проекционной связи с П₁ на П₂.

3) Проводим вспомогательные горизонтальные линии на П₂. Эти линии являются следами горизонтальных плоскостей, в которых перемещаются точки A и B;

4) Находим проекцию A₂'B₂' прямой A'B' на П₂, как точки пересечения линий связи с горизонтальными линиями.

Прямая AB спроецировалась на П₂ в натуральную величину, так как она параллельна ей. При перемещении угол а наклона AB к П₁ не изменился, так как перемещение происходило в горизонтальной плоскости. И теперь его можно определить по полученной проекции A₂'B₂' на П₂.

б) способ вращения вокруг оси, перпендикулярной к плоскости проекций.

Геометрическую фигуру вращают вокруг оси, перпендикулярной плоскости проекций, так, чтобы получить частное положение относительно тех же плоскостей проекций. Этот способ для решения некоторых задач более удобен, чем способ замены плоскостей проекций.

Рассмотрим свойства чертежа на примере вращения точки А вокруг оси m, перпендикулярной П₁ (рис. 5.8). Согласно закону вращения, точка А поворачивается вокруг оси m в плоскости s, которая перпендикулярна оси m по дуге окружности, центр которой О принадлежит оси вращения m (О m) на угол поворота g. Поскольку m ⊥ П₁, а s m, то s ǁ П₁.

Свойства чертежа (рис. 5.9):

1) Первая проекция точки А перемещается по дуге окружности с центром в точке О₁ = m₁, в которую проецируется ось вращения m. Радиус вращения равен длине отрезка (АО), а на чертеже (А₁О₁).

2) Вторая проекция точки А перемещается по прямой s₂, перпендикулярной проекции оси вращения m₂ (s₂ ⊥ m₂).

в) способ вращения вокруг оси, параллельной плоскости проекций (вращение вокруг линий уровня);

Этот способ применяется в основном для решения задачи преобразования плоскости общего положения в плоскость уровня. Суть способа заключается в том, что плоскость общего положения, поворачивается вокруг прямой уровня до состояния, параллельного либо горизонтальной П₁ либо фронтальной П2 плоскостям проекций.

Вращение точки

Рассмотрим поворот точки А вокруг горизонтали h до уровня горизонтали (рис. 5.13,а). Точка А движется по дуге окружности радиуса R с центром в точке O, принадлежащей горизонтали h. Радиус R является гипотенузой прямоугольного треугольника А₀АO, где один катет А₀О — горизонтальная проекция радиуса вращения, другой равен Z — расстоянию между точкой A и горизонтальной плоскостью, в которой лежит h. А' — новое положение точки А.

Алгоритм графических построений

1) Даны точки А(А₁,А₂) и горизонтальная прямая h(h₁,h₂). Через А₁ проводим горизонтальную проекцию плоскости вращения по которой поворачивается точка А. Это будет прямая, перпендикулярная прямой h₁ и проходящая через А₁.

2) На пересечении прямой h₁ и проекции плоскости вращения отмечаем точку O₁;

3) Строим прямоугольный треугольник A₁A₀O₁. Катет A₁A₀ равен Z, а гипотенуза A₀O₁ определяет расстояние между прямой h и точкой А. Отрезок A₀O₁ — расстояние R от точки A до прямой h;

4) Проводим дугу A₀A₁' с центром в точке O₁ А₁' — новая проекция точки А;

5) Подняв от A₁' линию проекционной связи до пересечения с h₂ находим A₂'.