Построение прямой, параллельной плоскости; прямой, перпендикулярной плоскости. Построение взаимно параллельных плоскостей.

Для того чтобы провести через точку А прямую параллельную плоскости α необходимо:
1) в плоскости α выбрать или построить произвольную прямую;
2) через точку А провести новую прямую параллельную выбранной прямой.

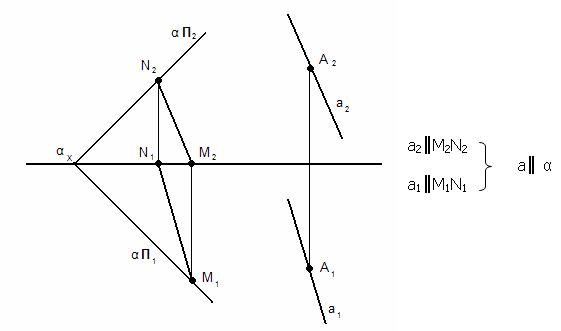
Для того чтобы проверить, параллельна ли прямая плоскости необходимо попытаться в заданной плоскости построить прямую параллельную заданной. Если это удастся, то прямая и плоскость параллельны.

Алгоритм построения перпендикуляра к плоскости

Вербальная форма	Графическая форма
1. Для того чтобы построить перпендикуляр к плоскости Р(DАВС) через точку D, необходимо сначала построить любую горизонталь в данной плоскости Р(D АВС) – h (h1h2)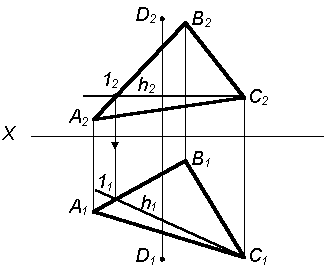

 

2. Строим фронталь в плоскости Р(D АВС) – f ( f1f2)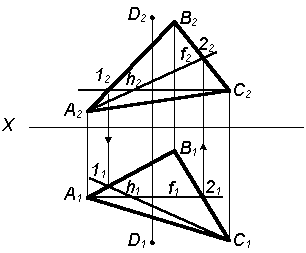
3. Строим перпендикуляр n к плоскости Р(DАВС). Для этого через точку D2 проводим n2, перпендикулярно f2, а через D1проводим n1, перпендикулярно h1. n (n1n2) ^Р (DАВС), так как n1^h1; h1 P1 ( DА1В1С1) n2^f2; f2 P2 (DА2В2С2)

Построение чертежа двух параллельных плоскостей основано на теореме стереометрии: если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны. Следовательно, чтобы построить плоскость Г', параллельную плоскости Г(АВС), достаточно провести через точку М две прямые, соответственно параллельные каким-нибудь двум пересекающимся прямым, принадлежащим плоскости Г, например сторонам (АВ) и (ВС) (рис. 4.8).
Рис. 4.8

Плоскость Г'(а b) параллельна плоскости Г(АВС), так как а (АВ) и b (ВС). Можно задать новую плоскость какими-нибудь другими пересекающимися прямыми, например горизонталью и фронталью, соответственно параллельными горизонтали и фронтали плоскости Г(АВС). Такая плоскость на рис. 4.8 проведена через точку N - плоскость (h' f') параллельна плоскости Г(АВС), так как h' h и f' f.