Интегрирование иррациональных функций. Первая подстановка Эйлера.
R(u1,…,un) =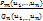 
Допустим, что в свою очередь переменные u1, …, un – сами являются функциями: u1 = f1(x), …, un = fn(x). Тогда ф-я R(f1(x),…, fn(x)) называется рациональной ф-ей от функций f1(x),…, fn(x).
Рассмотрим случай, когда интегрирование иррациональных ф-й можно свести с помощью некоторой подстановки к интегралу рациональных ф-й.
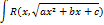
Этот интеграл сводится к интегрированию от рациональных
ф-й другой переменной следующей подстановкой:
1-я подстановка Эйлера а>0
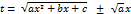
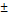- Будет одинаково
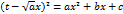
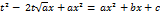
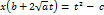
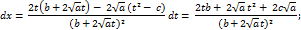
Затем подставляем под интеграл.