Питома (на одиницю ваги вагона) енергія вагона становить

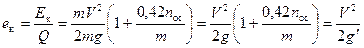. (1.10)

Величина 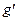в (1.10) являє собою приведене прискорення вільного падіння з урахуванням енергетичного впливу маси колісних пар, що обертаються,

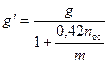, (1.11)

де m- маса вагона, т.

Таким чином, диференційне рівняння ( 1.9) для опису руху вагона як системи можна записати:

.

Фізичне рівняння руху вагона можна отримати шляхом інтегрування останнього:

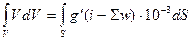. (1.12)

Інтегрування (1.12) в явному вигляді визнано неможливим. Достатньо точне для виконання інженерних розрахунків рішення можна отримати, якщо на елементарному переміщенні DS £ 10 м розглядати питомі сили як сталі величини.

В результаті, рівняння руху вагона буде мати вигляд

,

звідки . (1.13)

З допомогою виразу (1.13), як рекурентного, можливо розрахувати швидкість вагона в кінці кожної з достатньо малих послідовних ділянок DS маршрута, і отримати залежність V=f(S). При відносно малих DS ( не більше 5 м) тривалість скочування вагона t на кожному кроці можна визначити через середню швидкість, тобто

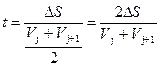. (1.14)

Підсумовуючи величини t на послідовних ділянках DS

T_j+1 = T_j + t_j,j+1 , (1.15)

можна отримати залежність тривалості скочування вагона від ВГ до будь-якої точки T = f(S).