Элементы комбинаторики. Применение комбинаторики к вычислению вероятности.

Правило произведения. Пусть элемент х₁ строки (х₁, х₂, …, х_k) можно выбрать n₁ способами; после каждого выбора х₁ элемент х₂ можно выбрать n₂ способами; после выборов х₁ и х₂ элемент х₃ можно выбрать n₃ способами и т.д.; после выборов х₁, х₂, …, х_k-1 элемент х_k можно выбрать n_k способами. Тогда строку (х₁, х₂, …, х_k) можно образовать n₁ × n₂ × … × n_k способами.

Пример.

Сколькими способами можно выбрать четырехзначное число, все цифры которого различны?

Решение.

Каждому четырехзначному числу можно поставить во взаимно однозначное соответствие строку (х₁, х₂, х₃, х₄), где х₁, х₂, х₃, х₄ – соответственно 1, 2, 3 и 4-я цифры. Элемент х₁ этой строки можно выбрать 9 способами (любую из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9); элемент х₂ можно выбрать также 9 способами (теперь можно использовать и цифру 0, но первую выбранную цифру повторить нельзя); элемент х₃ можно выбрать 8 способами (уже выбранные первые две цифры повторить нельзя); наконец, элемент х₄ можно выбрать 7 способами. Согласно правилу произведения искомое число способов выбора четырехзначного числа с различными цифрами равно: 9 × 9 × 8 × 7 = 4536.

Размещения с повторениями. Пусть Х – множество, состоящее из n элементов (n-членное множество). Тогда любая строка длиной k, составленная из элементов множества Х, называется размещением с повторениями из n элементов по k.

Число всех размещений с повторениями из n элементов по k равно n^k.

 

Пример.

Сколькими способами можно выбрать четырехзначное число, в десятичной записи которого нет нуля?

Решение.

Четырехзначные числа указанного вида можно рассматривать как строки длиной 4, составленные из элементов множества Х = {1, 2, 3, 4, 5, 6, 7, 8, 9}, т.е. как размещения с повторениями из 9 элементов по 4. Следовательно, искомое число способов равно: 9⁴ = 6561.

Размещения без повторений. Перестановки. Пусть Х по-прежнему n-членное множество. Тогда любая строка длиной k, составленная из различных элементов множества Х, называется размещением без повторений из n элементов по k. Число всех таких размещений обозначается и равно:

.

В случае, когда k = n, размещения без повторений называются перестановками из n элементов. Число всех перестановок из n элементов обозначается P_n и равно:

P_n = = n!.

Пример.

10 спортсменов разыгрывают одну золотую, одну серебряную и одну бронзовую медали. Сколькими способами эти медали могут быть распределены между спортсменами?

Решение.

Предположим, что спортсмены пронумерованы числами от 1 до 10 и х₁, х₂, х₃ – номера спортсменов, получивших золотую, серебряную и бронзовую медали. Каждому такому распределению медалей соответствует строка (х₁, х₂, х₃ ), состоящая из различных чисел (номеров спортсменов). Обратно каждой строке (х₁, х₂, х₃) соответствует способ распределения медалей. Следовательно, число способов распределения медалей равно числу размещений без повторений из 10 элементов по 3, т.е.

Сочетания. Всякое k-членное подмножество n-членного множества называется сочетанием из n элементов по k.

Число различных сочетаний из n элементов по k обозначается 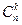. Справедлива формула

.

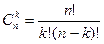Числа , , ,…, , являются коэффициентами в разложении бинома Ньютона:

(a + b)ⁿ = a⁰ bⁿ + a b^n-1 + … + aⁿ b⁰.

Пример.

Сколькими способами из 10 спортсменов можно отобрать команду из 6 человек?

Решение.

Очевидно, команда из 6 человек является 6-членным подмножеством 10-членного множества, т.е. сочетанием из 10 элементов по 6. Следовательно, искомое число способов равно

Размещения данного состава. Полиномиальная формула. Размещением данного состава (k₁, k₂,…, k_m) из элементов m-членного множества Х = {x₁, x₂ ,…, x_m} называется всякая строка длинной k₁ + k₂ + … + k_m = n, составленная из элементов множества Х, так, что элемент х₁ повторяется k₁ раз, элемент x₂ – k₂ раз и т.д., элемент x_m – k_m раз. Например, если Х= {x₁, x₂ ,x₃}, то (x₁, x₂ , x₂, х₁, х₁) есть размещение состава (3,2,0).

Количество различных размещений заданного состава (k₁, k₂,…, k_m) обозначается А(k₁, k₂,…, k_m) и равно:

.

Следующая формула, обобщающая формулу бинома Ньютона, называется полиномиальной:

,

где суммирование проводится по всевозможным наборам целых неотрицательных чисел k₁, k₂,…, k_m , для которых k₁ + k₂ + … + k_m = n.

Пример.

Сколькими способами можно поставить на книжной полке 3 экземпляра учебника по алгебре, 2 экземпляра учебника по геометрии и один экземпляр учебника по математическому анализу?

Решение.

Очевидно, всякой расстановке указанных учебников взаимно однозначно соответствует строка длиной 3 + 2 + 1 = 6 состава (3, 2,1). Следовательно, искомое число способов равно числу размещений состава (3, 2, 1) .т.е.

Если из совокупности объема n производится выборка k элементов с возвращением, то вероятность получения каждой конкретной выборки считается равной .

Если выборка производится без возвращения, то эта вероятность равна .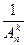

Пусть наступление события А состоит в появлении выборки с какими-то дополнительными ограничениями и количество таких выборок равно m. Тогда в случае выборки с возвращением имеем:

,

в случае выборки без возвращения:

.

Пример.

Наудачу выбирается трехзначное число, в десятичной записи которого нет нуля. Какова вероятность того, что у выбранного числа ровно две одинаковые цифры?

Решение.

Представим себе, что на 9 одинаковых карточках написаны цифры 1, 2, 3, 4, 5, 6, 7, 8, 9 и эти карточки помещены в урну. Выбор наудачу трехзначного числа равносилен последовательному извлечению с возвращением из урны 3 карточек и записыванием цифр в порядке их появления. Следовательно, число всех элементарных исходов опыта равно 9³ = 729. Количество благоприятных случаев для интересующего нас события А подсчитываем так: 2 различные цифры х и у можно выбрать способами; если х и у выбраны, то из них можно составить , т.е. 3 трехзначных числа, в которых х встречается два раза, а у –один раз; столько же будет чисел, в которых у встречается дважды; х – один раз. Таким образом, число благоприятных случаев равно 36 × (3 + 3) = 216. Искомая вероятность равна:

.

Пример.

Из букв слова «ротор», составленного с помощью разрезной азбуки, наудачу последовательно извлекаются 3 буквы и складываются в ряд. Какова вероятность того, что получится слово «тор»?

Решение.

Чтобы отличать одинаковые буквы друг от друга, снабдим их номерами: р₁, р₂, о₁, о₂. Тогда общее число элементарных исходов равно: . Слово «тор» получится в 1 × 2 ×2 = 4 случаях (то₁р₁, то₁р₂, то₂р₁, то₂р₂). Искомая вероятность равна: .

При подсчете числа благоприятных случаев мы здесь воспользовались правилом произведения: букву «т» можно выбрать одним способом, букву «о» – двумя и букву «р» – двумя способами.

Пример.

В партии из N деталей имеется n бракованных. Какова вероятность того, что среди наудачу отобранных k деталей окажется s бракованных?

Решение.

Количество всех элементарных исходов равно 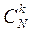. Для подсчета числа благоприятных случаев рассуждаем так: из n бракованных можно выбрать s деталей способами, а из N - n небракованных можно выбрать k – s небракованных деталей способами; по правилу произведения число благоприятных случаев равно × . Искомая вероятность равна:

.

Пример.

В бригаде 4 женщины и 3 мужчин. Среди членов бригады разыгрываются 4 билета в театр. Какова вероятность того, что среди обладателей билетов окажется 2 женщины и 2 мужчин?

Решение.

Применим схему статистического выбора. Из 7 членов бригады 4 человека можно выбрать = 35 способами, следовательно, число всех элементарных исходов испытания равно 35. Далее, из 4 женщин можно выбрать 2 женщины = 6 способами, а из 3 мужчин можно выбрать 2 мужчин 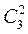= 6 способами, а из 3 мужчин можно выбрать 2 мужчин 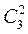= 3 способами. Тогда число благоприятных случаев будет равно 6 × 3 = 18. Таким образом, .