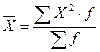Характеристика середньої геометричної та середньої квадратичної величини.
Якщо визначальна властивість сукупності формується як добуток індивідуальних значень ознаки, використовується середня геометрична:
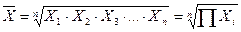 ,
,
де 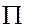 – символ добутку;
– символ добутку;
Xi – відносні величини динаміки, виражені кратним відношенням i-го значення показника до попереднього (i-1)-го.
Коли часові інтервали не однакові, розрахунок виконують за формулою середньої геометричної зваженої:
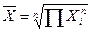
Найбільш широко використовується при аналізі динаміки з метою визначення середнього темпу зростання.
Середня квадратична використовується при визначенні показників варіації.
Середня квадратична проста:

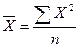
Середня квадратична зважена: