Промежуточные вычисления с использованием логарифмов исходных данных
| Y | X | YX | Y2 | X2 | ŷ | у – ŷ | (у – ŷ)2 | Ai | |
| 1,8376 | 1,6542 | 3,0398 | 3,3768 | 2,7364 | 61,0 | 7,8 | 60,8 | 11,3 | |
| 1,7868 | 1,7709 | 3,1642 | 3,1927 | 3,1361 | 56,3 | 4,9 | 24,0 | 8,0 | |
| 1,7774 | 1,7574 | 3,1236 | 3,1592 | 3,0885 | 56,8 | 3,1 | 9,6 | 5,2 | |
| 1,7536 | 1,7910 | 3,1407 | 3,0751 | 3,2077 | 55,5 | 1,2 | 1,4 | 2,1 | |
| 1,7404 | 1,7694 | 3,0795 | 3,0290 | 3,1308 | 56,3 | -1,3 | 1,7 | 2,4 | |
| 1,7348 | 1,6739 | 2,9039 | 3,0095 | 2,8019 | 60,2 | -5,9 | 34,8 | 10,9 | |
| 1,6928 | 1,7419 | 2,9487 | 2,8656 | 3,0342 | 57,4 | -8,1 | 65,6 | 16,4 | |
| Итого | 12,3234 | 12,1587 | 21,4003 | 21,7078 | 21,1355 | 403,5 | 1,7 | 197,9 | 56,3 |
| Среднее значение | 1,7605 | 1,7370 | 3,0572 | 3,1011 | 3,0194 | Х | х | 28,27 | 8,0 |
| σ | 0,0425 | 0,0484 | х | х | х | Х | х | х | х |
| σ2 | 0,0018 | 0,0023 | х | х | х | Х | х | х | х |
Рассчитаем С (или lg a) и b:
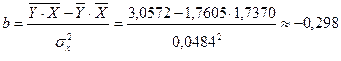
Получим линейное уравнение: Ŷ = 2,278 – 0,298Х. Выполнив его потенцирование, перейдем к следующему виду:
.
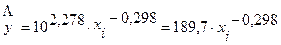Подставляя в данное уравнение фактические значения хi, получаем теоретические значения результата ŷi. По ним рассчитаем показатели: тесноты связи – индекс корреляции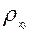 
и среднюю ошибку аппроксимации 
:
= 
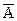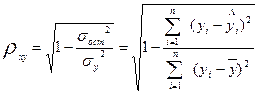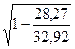= 0,3758,
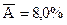
Характеристики степенной модели указывают, что она несколько лучше линейной функции описывает взаимосвязь.
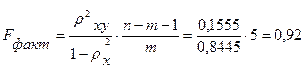
Где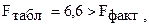 
при уровне значимости α = 0,05
Следовательно, принимается гипотеза Но о статистически незначимых параметрах этого уравнения. Этот результат можно объяснить сравнительно невысокой теснотой выявленной зависимости и небольшим числом наблюдений.
1.3. Показательная функция: ŷ = а bx
Уравнение регрессии показательной функции: ŷ = 77,24 * 0,9947х.
Решение аналогично предыдущей задаче 1.2
Задача 2.
По совокупности 30 предприятий торговли изучается зависимость между признаками: х – цена за товар А, тыс. руб, у – прибыль торгового предприятия, млн. руб. При оценке регрессионной модели были получены следующие промежуточные результаты.
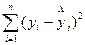=39000
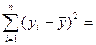120000
▪ Поясните, какой показатель корреляции можно определить по этим данным.
▪ Проведите дисперсионный анализ для расчета F-критерия Фишера.
Для вычислений будем использовать следующие формулы:
- общая сумма квадратов отклонений;
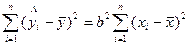– сумма квадратов отклонений, обусловленная регрессией;
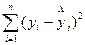– остаточная сумма квадратов отклонений.
▪ Сравните фактическое значение F-критерия с табличным. Сделайте выводы.
Решение.
▪ По указанным данным можно определить индекс корреляции рху для нелинейной регрессии:
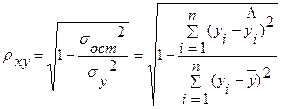= 0,822
, 
, 
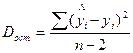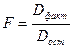или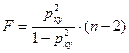 
.
Dфакт=120000-39000=81000; Dост=39000/28=1393; тогда F = 58 или
▪ 
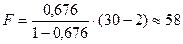
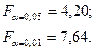
Поскольку Fфакт>Fтабл как при 1%-ном, так и при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии.
Задача 3.
Для трех видов продукции А, В и С модели зависимости удельных постоянных расходов от объема выпускаемой продукции выглядит следующим образом:
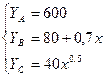
▪ Определите коэффициент эластичности по каждому виду продукции и поясните их смысл.
▪ Каким должен быть объем выпускаемой продукции, чтобы коэффициенты эластичности для продукции В и С были равны.
Решение.
Коэффициент эластичности функции В зависит от значений фактора х.
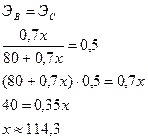
Объем выпускаемой продукции в случае равенства коэффициентов эластичности для продукции В и С должен быть равен 114,3.