Вычисления для линейной функции

	y	x	yx	x²	y²	ŷ	у – ŷ	A_i
	68,8	45,1	3102,88	2034,01	4733,44	61,3	7,5	10,9
	61,2	59,0	3610,80	3481,00	3745,44	56,5	4,7	7,7
	59,9	57,2	3426,28	3271,84	3588,01	57,1	2,8	4,7
	56,7	61,8	3504,06	3819,24	3214,89	55,5	1,2	2,1
	55,0	58,8	3234,00	3457,44	3025,00	56,5	-1,5	2,7
	54,3	47,2	2562,96	2227,84	2948,49	60,5	-6,2	11,4
	49,3	55,2	2721,36	3047,04	2430,49	57,8	-8,5	17,2
Итого	405,2	384,3	22162,34	21338,41	23685,76	405,2	0,0	56,7
Среднее значение	57,89	54,90	3166,05	3048,34	3383,68	х	х	8,1
σ	5,74	5,86	х	х	х	х	х	х
σ²	32,92	34,34	х	х	х	х	х	х

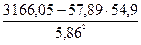
b = = 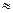-0,35

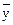a = - b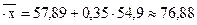

Уравнение регрессии: ŷ = 76,88-0,35 х.

С увеличением среднедневной заработной платы на 1 руб. доля расходов на покупку продовольственных товаров снижается в среднем на 0,35 %-ых пункта.

Для определения направления и тесноты связи рассчитаем линейный коэффициент парной корреляции:

Связь по тесноте умеренная, по направлению - обратная.

Определим коэффициент детерминации. Для этого:

· можно рассчитать по формуле R^{2 =}r_xy² = (-0,357)² = 0,127.

· получить в рамках оценивания параметров регрессии на компьютере Вариация результата на 12,7 % объясняется вариацией фактора х.

Подставляя в уравнение регрессии фактические значения х_i, определим теоретические (расчётные) значения ŷ_i. Найдём величину средней ошибки аппроксимации 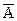. Проведем расчеты согласно формуле, промежуточные вычисления даны в таблице 4.

`

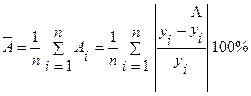
`А = 8,1 %. В среднем расчётные значения отклоняются от фактических на 8,1 %.

Рассчитаем F-критерий Фишера:

· через коэффициент детерминации R² по формуле:

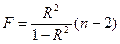
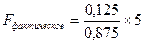= 0,714

Критические значения берутся из статистических таблиц согласно приведенному в теоретической части построению.

F_{критическое при}_a=1% = 16,26

F_{критическое при}_a=5% = 6,61

F_{фактическое}> F_{критическое при}_a=5%Гипотеза H₀не принимается при 5% -ом уровне значимости, что говорит о значимости уравнения регрессии в целом.

F_{фактическое}< F_{критическое при}_a=1%. Полученное значение указывает на необходимость принять гипотезу H₀о случайной природе выявленной зависимости и статистической незначимости параметров уравнения и показателя тесноты связи.

· значение F-статистики можно получить в рамках оценивания регрессии, что будет продемонстрировано далее в рамках проведения регрессионного анализа на компьютере с использованием встроенных функций.

2. Степенная модель: ŷ = a х^b.

Проведём процедуру линеаризации путём логарифмирования обеих частей уравнения:

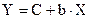
где Y = lg y, X = lg x, C = lg a.

Таблица 5