Схема дисперсионного анализа.

Компоненты дисперсии	Сумма квадратов	Число степеней свободы	Средние квадраты
Регрессия		m – 1	Dфакт =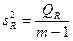
Остаточная		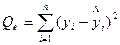n – m	Dост =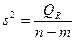
Общая		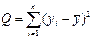n – 1

 

Средние квадраты 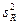и s² представляют собой несмещенные оценки зависимой переменной, обусловленные соответственно регрессией или объясняющей переменной х и воздействием неучтенных случайных факторов и ошибок; m – число оцениваемых параметров регрессии, n – число наблюдений.

При отсутствии линейной зависимости между зависимой и объясняющей(ими) переменной случайные величины 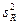и s² имеют c² – распределение соответственно с (m-1) и (n-m) степенями свободы, а их отношение - F – распределение с теми же степенями свободы. Поэтому, уравнение регрессии значимо на уровне a, если фактически наблюдаемое значение статистики больше F_{a, k1, k2}:

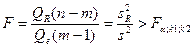, (26)

где 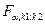- табличное значение F – критерия Фишера, определенное на уровне значимости a при k1 = m-1 и k2 = n-m числе степеней свободы.

Учитывая смысл величин 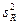и s², можно сказать, что значение F показывает, в какой мере регрессия лучше оценивает значение зависимой переменной по сравнению с ее средней.

В случае парной линейной регрессии m = 2, и уравнение регрессии значимо на уровне a, если

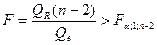(27)

В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка, называемая стандартной ошибкой коэффициента.

Оценки истинных, но неизвестных, значений параметров – это числа, зависящие от количества и состава наблюдений, т.е.от выборки. При различных выборках мы получили бы различные оценки. Если продолжать брать все больше выборок и получать дополнительные оценки, то оценки каждого параметра будут соответствовать некоторому распределению вероятностей., которое может быть суммировано как среднее и мера дисперсии, следовательно, сравниваемые параметры распределены нормально. Нормальное распределение имеет следующее свойство: область, находящаяся в пределах 1,96 стандартного отклонения от его среднего значения составляет 95% всей области. Учитывая это, можно указать такой интервал вокруг оценки параметра, что с вероятностью 95 %истинное значение параметра лежит внутри этого интервала. Данный интервал, называемый 95-% -ным доверительным интервалом определяется так:

b ± 1,96 среднего квадратического отклонения от b

Можно проверить гипотезу о том, что истинное значение параметра равно нулю, изучая ее t – статистику, котораяопределяется следующим образом:

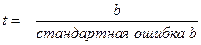(28)

В ряде прикладных задач требуется оценить значимость коэффициента корреляции r. При этом исходят из того, что при отсутствии корреляционной связи t - статистика, найденная по формуле имеет t- распределение Стьюдента с (n-2) степенями свободы.

Коэффициент корреляции r_xy значим на уровне a, (иначе – гипотеза Н₀ о равенстве генерального коэффициента корреляции нулю отвергается), если

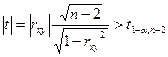, (29)

где 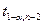- табличное значение t- критерия Стьюдента, определенное на уровне значимости a при числе степеней свободы (n-2).

Процедура оценивания существенности коэффициента корреляции не отличается от рассмотренной выше для коэффициента регрессии: вычисляется значение t-критерия, его величина сравнивается с табличным значением при (n-2) степенях свободы.

Проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.