И корреляции. F-критерий Фишера. Дисперсионный анализ
После построения уравнения линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.
Проверить значимость уравнения регрессии – это установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.
Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, следовательно, фактор х не оказывает влияния на результат у.
Величина F–отношения (F-критерий) получается при сопоставлении факторной и остаточной дисперсии в расчете на одну степень свободы.
F= Dфакт / Dост (19)
F-критерий проверки для нулевой гипотезы
Н0: Dфакт = Dост (20)
Если нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для Н0 необходимо опровержение, если факторная дисперсия превышает остаточную в несколько раз.
Английским статистиком Снедекором разработаны таблицы критических значений F-отношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы. Табличное значение F-критерия – это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения признается достоверным (отличным от 1), если оно больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: если Fфакт > Fтабл , то Н0 отклоняется.
Если же величина оказалась меньше табличной Fфакт < Fтабл, то вероятность нулевой гипотезы меньше заданного уровня (например, 0, 05) и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи.
Проверка значимости уравнения регрессии производится на основе дисперсионного анализа. В математической статистике дисперсионный анализ рассматривается как самостоятельный инструмент (метод) статистического анализа. В эконометрике же он применяется как вспомогательное средство для изучения качества модели. Центральное место в анализе дисперсии занимает разложение общей суммы квадратов отклонений переменной у от среднего значения `у на 2 части - «объясненную» и «необъясненную»и может быть представлена следующим образом:
| Общая сумма квадратов отклонений | = | Сумма квадратов отклонений, объясненная регрессией | + | Остаточная сумма квадратов отклонений |
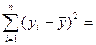

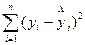 (21) ,
(21) ,
где 
или
Q = QR + Qe (22),
где Q - общая сумма квадратов отклонений;
QR - сумма квадратов отклонений, обусловленная регрессией;
Qe– остаточная сумма квадратов отклонений.
Q =  (23)
(23)
QR = 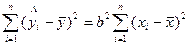 (24)
(24)
Qe = 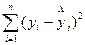 (25)
(25)
Таблица 2.