Учет (дисконтирование) по сложной ставке процентов

Здесь, также как и в случае простых процентов, будут рассмотрены два вида учета - математический и банковский.

Математический учет. В этом случае решается задача обратная наращению по сложным процентам. Запишем исходную формулу для наращения

S=P(1+i)ⁿ

и решим ее относительно P

, (35)

где

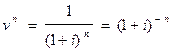(36)

учетный или дисконтный множитель.

Если проценты начисляются m раз в году, то получим

, (37)

где

(38)

дисконтный множитель.

Величину P, полученную дисконтированием S, называют современной или текущей стоимостью или приведенной величиной S. Суммы P и S эквивалентны в том смысле, что платеж в сумме S через n лет равноценен сумме P, выплачиваемой в настоящий момент.

Разность D=S-P называют дисконтом.

Банковский учет. В этом случае предполагается использование сложной учетной ставки. Дисконтирование по сложной учетной ставке осуществляется по формуле

P=S(1-d_сл)ⁿ, (39)

где d_сл - сложная годовая учетная ставка.

 

Дисконт в этом случае равен

 

D=S-P=S-S(1-d_сл)ⁿ=S[1-(1-d_сл)ⁿ]. (40)

 

При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, так как учетная ставка каждый раз применяется к сумме, уменьшенной за предыдущий период на величину дисконта.